Code documentation

Module API

Module defining class Microstructure that contains the necessary methods and attributes to analyze experimental microstructures in form of EBSD maps to generate statistical descriptors for 3D microstructures, and to create synthetic RVE that fulfill the required statistical microstructure descriptors.

The methods of the class Microstructure for an API that can be used to generate Python workflows.

Authors: Alexander Hartmaier, Golsa Tolooei Eshlghi, Abhishek Biswas Institution: ICAMS, Ruhr University Bochum

class kanapy.core.api.Microstructure(descriptor=None, file=None, name='Microstructure')

Bases: object

Define a class for creating and managing synthetic microstructures

This class provides tools to define, generate, and analyze synthetic microstructures composed of one or multiple phases. It integrates particle packing, voxelization, and grain geometry generation for RVE (Representative Volume Element) modeling.

Parameters

descriptorlist of dict, optional

List of dictionaries describing the microstructure of each phase. Dictionary keys typically include “Grains type”, “Equivalent diameter”, “Aspect ratio”, “Tilt Angle”, “RVE”, and “Simulation”.

filestr, optional

Path to a JSON or other input file to initialize the microstructure.

namestr, default=’Microstructure’

Name of the microstructure

Attributes

namestr

Name of the microstructure

nphasesint or None

Number of phases in the microstructure

ngrainsndarray or None

Array of grain counts in each phase

nparticleslist or None

List of the number of particles in each phase

descriptorlist of dict or None

Descriptor used to define microstructure if provided

precipitfloat or None

Indicates the presence of precipitates, pores, or secondary particles in a continuous matrix. If float, specifies their volume fraction

from_voxelsbool

True if the microstructure is imported from a voxel file

particleslist or None

List of particle objects containing geometric information

rveRVE_creator or None

Object containing RVE information including mesh dimensions, particle count, periodicity, and phase volume fractions

simboxSimulation_Box or None

Object defining the geometric boundaries of the RVE simulation domain

meshmesh_creator or None

Object storing voxelized mesh data including grain assignments, voxel connectivity, and smoothed node coordinates

geometrydict or None

Dictionary of grain geometries. Keys may include “Vertices”, “Points”, “Simplices”, “Facets”, “Grains”, “GBnodes”, “GBarea”, “GBfaces”

rve_statslist of dict or None

Statistical information for different RVE representations, including particles, voxels, and polyhedral grains

rve_stats_labelslist of str or None

Labels corresponding to the types of RVEs analyzed, e.g., “Particles”, “Voxels”, “Grains”

vf_voxndarray or None

Phase volume fractions obtained from voxelized structures

ialloyint or None

Alloy identifier used for material library mapping

Notes

• The class can initialize from either a statistical descriptor or a JSON data file

• When only one phase is specified with a volume fraction < 1.0, a matrix phase is automatically added with a complementary fraction (1 - vf)

• Kanapy is tested for up to two phases; using more may yield unpredictable results

generate_grains()

Calculate and store polyhedral grain geometry, including particle- and grain-diameter attributes, for statistical comparison

Notes

• Requires self.mesh to be initialized by voxelize.

• Updates self.geometry with polyhedral grain volumes and shared grain boundary (GB) areas.

• If self.precipit is True, irregular grain 0 is temporarily removed from analysis.

• Logs warnings if grains are not represented in the polyhedral geometry.

• Prints volume fractions of each phase in the polyhedral geometry.

Parameters

None

Returns

None

The calculated grain geometry is stored in self.geometry. Phase volume fractions are printed to the console.

Raises

ValueError

• If self.mesh or self.mesh.grains is None (i.e., voxelized microstructure not available).

generate_orientations(data, ang=None, omega=None, Nbase=5000, hist=None, shared_area=None, iphase=None, verbose=False)

Generate orientations for grains in a representative volume element (RVE) to achieve a desired crystallographic texture

This method assigns grain orientations to achieve a specified texture. The input can be an EBSDmap object or a string defining the type of orientation set (random or unimodal). For unimodal textures, ang and omega must be specified. Generated orientations are stored in self.mesh.grain_ori_dict, and self.mesh.texture is updated accordingly.

Parameters

dataEBSDmap or str

Input source for orientations. Can be an EBSDmap object or a string specifying the type of orientation set: - ‘random’ or ‘rnd’ : generate a random orientation set - ‘unimodal’, ‘uni_mod’, or ‘uni_modal’ : generate a unimodal orientation set

angfloat, optional

Orientation angle for unimodal texture (required if data is unimodal).

omegafloat, optional

Kernel halfwidth for unimodal texture (required if data is unimodal).

Nbaseint, default=5000

Number of base orientations used in random or unimodal generation.

histarray_like, optional

Histogram for the grain orientations, used to weight orientations.

shared_areaarray_like or float, optional

Shared grain boundary area for weighted orientation generation.

iphaseint, optional

Phase index for which orientations are generated. If None, all phases are processed.

verbosebool, default=False

If True, prints additional information during orientation generation.

Returns

None

The generated orientations are stored in self.mesh.grain_ori_dict and self.mesh.texture is updated to reflect the type of generated texture.

Raises

ValueError

• If grain geometry is not defined (i.e., self.mesh.grains is None).

• If data is unimodal but ang or omega are not provided.

• If data is neither EBSDmap nor a recognized string option.

• If histogram is provided but GB areas are not defined (and shared_area is None).

Examples

>>> # Generate random orientations for all grains
>>> rve.generate_orientations('random')

>>> # Generate unimodal orientations with specified angle and halfwidth
>>> rve.generate_orientations('unimodal', ang=30.0, omega=10.0)

>>> # Generate orientations for a specific phase with histogram weighting
>>> rve.generate_orientations('random', hist=hist_array, iphase=1)

>>> # Generate orientations using an EBSDmap object
>>> rve.generate_orientations(ebsd_map_obj)

import_particles(file, path='./')

Import particle data from a dump file

This function reads particle information from a specified dump file and stores it in the microstructure object, updating the simulation box and particle list.

Parameters

filestr

Name of the input dump file containing particle data

pathstr, optional

Directory path where the dump file is located. Default is current directory ‘./’

Returns

None

Updates the object’s simbox and particles attributes

init_RVE(descriptor=None, nsteps=1000)

Initialize the Representative Volume Element (RVE) of the microstructure

This method creates the voxel- or particle-based RVE using the provided phase descriptor(s). It sets up the mesh dimensions, particle distribution, and simulation box geometry. The RVE object is constructed using the RVE_creator class, and key attributes such as nparticles and simbox are updated accordingly.

Parameters

descriptorlist of dict, dict, or None, optional

Description of the microstructure phases. Each dictionary specifies parameters such as grain type, equivalent diameter, aspect ratio, and tilt angle. If None, the class attribute self.descriptor is used.

nstepsint, optional

Number of optimization or relaxation steps for RVE generation. Default is 1000.

Notes

• Assumes that RVE_creator and Simulation_Box are available and correctly configured.

• If self.precipit is defined, an additional ‘Matrix’ phase is automatically added to preserve total volume fraction normalization.

Attributes Updated

rveRVE_creator

The created RVE object containing voxel/particle information, size, periodicity, and phase volume fractions.

nparticleslist

Number of particles per phase after RVE generation.

simboxSimulation_Box

Object containing the geometric boundaries of the RVE domain.

precipitfloat or None

If not None, a ‘Matrix’ phase is appended to rve.phase_names and its volume fraction is adjusted as (1.0 - precipit).

Returns

None

Updates class attributes with the initialized RVE and simulation box.

init_stats(descriptor=None, gs_data=None, ar_data=None, porous=False, save_files=False)

Legacy function that redirects to plot_stats_init

This function is deprecated and serves as a wrapper for plot_stats_init. A warning is logged advising users to use plot_stats_init directly.

Parameters

descriptorAny, optional

Descriptor data passed to plot_stats_init. Default is None.

gs_dataAny, optional

Grain size data passed to plot_stats_init. Default is None.

ar_dataAny, optional

Aspect ratio data passed to plot_stats_init. Default is None.

porousbool, optional

Deprecated parameter, ignored. Default is False.

save_filesbool, optional

Whether to save generated statistics files. Default is False.

Returns

None

Calls plot_stats_init and does not return any value

output_abq(nodes=None, name=None, voxel_dict=None, grain_dict=None, faces=None, dual_phase=False, thermal=False, units=None)

Legacy function that redirects to write_abq

This function is deprecated and serves as a wrapper for write_abq. Warnings are logged advising users to use write_abq directly. The faces parameter is determined automatically if provided.

Parameters

nodesarray-like, optional

Nodal coordinates to include in the output. Default is None.

namestr, optional

File name for the Abaqus input file. Default is None.

voxel_dictdict, optional

Voxel connectivity information. Default is None.

grain_dictdict, optional

Grain-to-voxel mapping. Default is None.

facesAny, optional

Deprecated parameter, automatically determined. Default is None.

dual_phasebool, optional

Whether to include dual-phase data. Default is False.

thermalbool, optional

Whether to include thermal data. Default is False.

unitsdict, optional

Dictionary of units for the Abaqus model. Default is None.

Returns

None

Calls write_abq and does not return any value

output_ang(ori=None, cut='xy', data=None, plot=True, cs=None, pos=None, fname=None, matname='XXXX', save_files=True, dual_phase=False, save_plot=False)

Convert microstructure orientations into a .ang file, optionally plotting a slice

This function generates a .ang file mimicking an EBSD map. If polygonalized microstructure is available, it will be used; otherwise, or if data=’voxels’, the voxelized microstructure will be exported. If no orientations are provided, each grain receives a random Euler angle. The function can also plot a 2D slice of the orientation map along a specified cutting plane.

Parameters

oriarray-like of shape (self.Ngr, 3), optional

Euler angles of grains. If None, random angles are generated.

cut{‘xy’, ‘xz’, ‘yz’}, optional

Plane along which to take a slice. Default is ‘xy’.

data{‘voxels’, ‘poly’}, optional

Basis for generating the ANG file. Default is None, automatically selected.

plotbool, optional

Whether to display a plot of the slice. Default is True.

csstr, optional

Crystal symmetry. Default is None.

posfloat or str, optional

Slice position as a numerical value or one of ‘top’, ‘bottom’, ‘left’, ‘right’. Default is None (uses top/right edge).

fnamestr, optional

Filename for the output ANG file. Default is generated automatically.

matnamestr, optional

Material name to write in the ANG file. Default is ‘XXXX’.

save_filesbool, optional

Whether to save the ANG file. Default is True.

dual_phasebool, optional

Whether to output dual-phase information. Default is False.

save_plotbool, optional

Whether to save the plot as a PDF. Default is False.

Returns

fnamestr

Name of the generated ANG file.

Raises

ValueError

• If pos is not a float or one of ‘top’, ‘bottom’, ‘left’, ‘right’.

• If cut is not ‘xy’, ‘xz’, or ‘yz’.

• If neither polygonal nor voxel microstructure is available.

Notes

• Uses Delaunay triangulation to determine which grain each pixel belongs to when exporting polygons.

• Slice plotting uses a colormap (default ‘prism’) and includes optional dual-phase coloring.

Examples

>>> # Export an XY slice with default settings
>>> fname = rve.output_ang(cut='xy')

>>> # Export a slice using voxel data and a specific Euler angles array
>>> fname = rve.output_ang(ori=euler_array, data='voxels', cut='xz', pos=10)

>>> # Plot and save the slice as PDF
>>> fname = rve.output_ang(save_plot=True)

output_neper()

Write particle position and weight files for Neper tessellation

This function generates two text files required for tessellation in Neper: - sphere_positions.txt containing the x, y, z coordinates of each particle - sphere_weights.txt containing the weight (radius) of each particle

The files are written in the current working directory. Each particle in self.particles is included in the output.

Raises

ValueError

If self.particles is None, indicating that particles have not been packed yet.

Notes

• Requires that particles are initialized via the pack() method.

• The particle dictionary is built internally but not returned.

Examples

>>> # Write Neper input files for current particles
>>> rve.output_neper()

pack(particle_data=None, k_rep=0.0, k_att=0.0, fill_factor=None, poly=None, save_files=False, verbose=False)

Pack particles into the simulation box according to the RVE settings.

Parameters

particle_dataarray-like or None, optional

Particle information. If None, uses self.rve.particle_data.

k_repfloat, optional

Repulsion coefficient between particles. Default is 0.0.

k_attfloat, optional

Attraction coefficient between particles. Default is 0.0.

fill_factorfloat or None, optional

Fraction of simulation box to fill. Defaults to 1.0 if self.precipit is set.

polyoptional

Additional packing options for polyhedral particles.

save_filesbool, optional

If True, saves packed particle data to files.

verbosebool, optional

If True, prints progress and warnings during packing.

Returns

particleslist

List of packed particle objects with positions and geometrical information.

simboxSimulation_Box

Updated simulation box reflecting particle packing.

Raises

ValueError

If no particle data is available.

AttributeError

If RVE or simulation box is not initialized before packing.

Notes

If self.precipit > 0.65, particle overlaps may occur. Requires self.rve and self.simbox to be initialized before calling.

pckl(file=None, path='./')

Write the microstructure into a pickle file

This function serializes the microstructure object using pickle, allowing complex structures to be stored and later reloaded.

Parameters

filestr, optional

File name for the pickled microstructure. If None, the filename defaults to the microstructure name plus ‘.pckl’.

pathstr, optional

Directory path to save the pickle file. Default is current directory ‘./’.

Returns

None

plot_ellipsoids(cmap='prism', dual_phase=None, phases=False)

Generate a 3D plot of particles in the RVE

This function visualizes ellipsoidal particles in the Representative Volume Element (RVE). Particles can be colored according to phase, and a custom colormap can be used. Note that dual_phase is deprecated; use phases instead.

Parameters

cmapstr, optional

Colormap used for plotting particles. Default is ‘prism’.

dual_phasebool or None, optional

Deprecated parameter for indicating dual-phase visualization. Use phases instead. Default is None.

phasesbool, optional

If True, color particles according to their phase. Default is False.

Notes

• Requires self.particles to be initialized by pack.

• Automatically calculates aspect ratios of the RVE for proper 3D plotting.

• Prints a warning if dual_phase is used and maps it to phases.

Returns

None

Displays a 3D plot of ellipsoidal particles using plot_ellipsoids_3D.

Raises

ValueError

• If self.particles is None.

Examples

>>> # Simple 3D plot with default colormap
>>> rve.plot_ellipsoids()

>>> # Color particles according to phase
>>> rve.plot_ellipsoids(phases=True)

>>> # Use a custom colormap
>>> rve.plot_ellipsoids(cmap='viridis')

plot_grains(geometry=None, cmap='prism', alpha=0.4, ec=None, dual_phase=None, phases=False)

Plot the polygonalized microstructure of the RVE in 3D.

This function visualizes the polygonal (polyhedral) grain geometry of the microstructure, typically after generate_grains() has been executed. Users can customize the colormap, transparency, and edge color. It also supports coloring grains by phase.

Parameters

geometrydict or None, optional

Dictionary containing the polygonal grain geometries. If None, uses self.geometry.

cmapstr, optional

Matplotlib colormap name for rendering grain colors. Default is ‘prism’.

alphafloat, optional

Transparency level of the grain surfaces (0 = fully transparent, 1 = fully opaque). Default is 0.4.

eclist or None, optional

Edge color specified as an RGBA list, e.g. [0.5, 0.5, 0.5, 0.1]. Default is [0.5, 0.5, 0.5, 0.1].

dual_phasebool or None, optional

Deprecated parameter for dual-phase coloring. Use phases instead. Default is None.

phasesbool, optional

If True, color grains by phase rather than by grain ID. Default is False.

Notes

• Requires polygonal grain data generated by generate_grains().

• Automatically computes the aspect ratio of the RVE for correct 3D scaling.

• Visualization is handled by plot_polygons_3D().

• The parameter dual_phase is deprecated; prefer using phases instead.

Returns

None

Displays a 3D plot of polygonal grains.

Raises

ValueError

If no polygonal geometry is available (i.e., self.geometry is None).

Examples

>>> # Simple 3D plot of polygonal grains with default settings
>>> rve.plot_grains()

>>> # Color grains by phase
>>> rve.plot_grains(phases=True)

>>> # Use a custom colormap and set transparency
>>> rve.plot_grains(cmap='viridis', alpha=0.6)

>>> # Specify edge color
>>> rve.plot_grains(ec=[0.2, 0.2, 0.2, 0.3])

plot_particles(cmap='prism', dual_phase=None, phases=False, plot_hull=True)

Generate a 3D plot of particles in the RVE.

This function visualizes particles in the Representative Volume Element (RVE) in 3D. Particles can be colored according to phase, plotted with their convex hulls, and displayed using a custom colormap.

Parameters

cmapstr, optional

Colormap used for plotting particles. Default is ‘prism’.

dual_phasebool or None, optional

Deprecated parameter for indicating dual-phase visualization. Use phases instead. Default is None.

phasesbool, optional

If True, color particles according to their phase. Default is False.

plot_hullbool, optional

If True, plot the convex hull (inner polygon) of each particle. Default is True.

Notes

• Requires self.particles to be initialized by pack.

• Automatically calculates aspect ratios of the RVE for proper 3D plotting.

• Prints a warning if dual_phase is used and maps it to phases.

Returns

None

Displays a 3D plot of particles using plot_particles_3D.

Raises

ValueError

• If self.particles is None.

• If particles do not have inner polygons.

Examples

>>> # Simple 3D plot with default colormap and convex hulls
>>> rve.plot_particles()

>>> # Color particles according to phase
>>> rve.plot_particles(phases=True)

>>> # Plot particles without convex hulls and use a custom colormap
>>> rve.plot_particles(cmap='viridis', plot_hull=False)

plot_slice(cut='xy', data=None, pos=None, fname=None, dual_phase=False, save_files=False)

Plot a 2D slice through the microstructure.

The function visualizes a cross-section of the microstructure. If a polygonalized microstructure is available, it will be used as the plotting basis; otherwise, or if data=’voxels’, the voxelized microstructure will be plotted. This method internally calls output_ang with plotting enabled and file writing disabled.

Parameters

cutstr, optional

The cutting plane of the slice. Options are ‘xy’, ‘xz’, or ‘yz’. Default is ‘xy’.

datastr, optional

Data basis for plotting. Options are ‘voxels’ or ‘poly’. Default is None.

posstr or float, optional

Position of the slice, either as an absolute value or as one of ‘top’, ‘bottom’, ‘left’, ‘right’. Default is None.

fnamestr, optional

Filename to save the figure as a PDF. Default is None.

dual_phasebool, optional

If True, enable dual-phase visualization. Default is False.

save_filesbool, optional

If True, the figure will be saved to disk. Default is False.

Returns

None

Examples

>>> micro.plot_slice(cut='xz', data='poly', pos='top', save_files=True)

plot_stats(data=None, gs_data=None, gs_param=None, ar_data=None, ar_param=None, dual_phase=None, phases=False, save_files=False, show_all=False, verbose=False, silent=False, enhanced_plot=False)

Plot particle, voxel, and grain diameter statistics for comparison

This method analyzes the microstructure at different representation levels (particles, voxels, and polyhedral grains) and plots corresponding statistical distributions. It can optionally handle multiphase materials, save plots, and display detailed information about geometric parameters.

Parameters

datastr or None, optional

Specifies which type of data to analyze and plot: - ‘p’ : particles - ‘v’ : voxels - ‘g’ : grains If None, all available data types are analyzed.

gs_datalist or array-like, optional

Grain size data for comparison with simulation results.

gs_paramlist or array-like, optional

Parameters for fitting grain size distributions.

ar_datalist or array-like, optional

Aspect ratio data for comparison with simulation results.

ar_paramlist or array-like, optional

Parameters for fitting aspect ratio distributions.

dual_phasebool or None, optional

Deprecated. Use phases instead.

phasesbool, optional

If True, perform separate statistical analysis for each phase.

save_filesbool, optional

If True, save generated plots and statistical results to files.

show_allbool, optional

If True, display all generated plots interactively.

verbosebool, optional

If True, print detailed numerical results during analysis.

silentbool, optional

If True, suppresses console output and returns figures directly.

enhanced_plotbool, optional

If True, use enhanced plot styling (automatically enabled when silent=True).

Returns

flistlist of matplotlib.figure.Figure or None

List of generated figure objects if silent=True, otherwise None.

Raises

None

This function does not raise exceptions if data is missing. Instead, it logs an error message and returns immediately.

Notes

• Computes and compares geometric parameters such as principal axis lengths (a, b, c), aspect ratios, rotation axes, and equivalent diameters.

• Results are stored in self.rve_stats and labeled in self.rve_stats_labels.

• For multiphase structures, statistics are calculated per phase.

• dual_phase is deprecated; prefer using phases.

Examples

>>> # Plot all statistics with default settings
>>> rve.plot_stats()

>>> # Plot only particle statistics and show all plots interactively
>>> rve.plot_stats(data='p', show_all=True)

>>> # Perform multiphase statistical analysis and save figures
>>> rve.plot_stats(phases=True, save_files=True)

>>> # Suppress console output and get figure objects
>>> figs = rve.plot_stats(silent=True)

plot_stats_init(descriptor=None, gs_data=None, ar_data=None, porous=False, get_res=False, show_res=False, save_files=False, silent=False, return_descriptors=False)

Plot initial statistical microstructure descriptors of RVE and optionally return computed descriptors

This method analyzes the initial microstructure defined by input descriptors (or the class attribute self.descriptor) and plots the distributions of equivalent diameters and aspect ratios. For elongated grains, it prints a summary of input and output statistics. Optionally, statistical descriptors can be returned for further processing.

Parameters

descriptorlist of dict, dict, or None, optional

Microstructure phase descriptor(s). If None, uses self.descriptor.

gs_datalist or array-like, optional

Grain size data for comparison with initial statistics.

ar_datalist or array-like, optional

Aspect ratio data for comparison with initial statistics.

porousbool, optional

If True, only the first phase is considered (e.g., for porous structures).

get_resbool, optional

If True, computes statistical descriptors from the voxelized structure.

show_resbool, optional

If True, prints detailed statistical results to the console.

save_filesbool, optional

If True, saves generated plots to files.

silentbool, optional

If True, suppresses console output and returns figures directly.

return_descriptorsbool, optional

If True, returns computed statistical descriptors along with figures.

Returns

flistlist of matplotlib.figure.Figure

List of generated figure objects.

descslist of dict

Optional list of computed statistical descriptors if return_descriptors=True.

Notes

• Requires voxelized microstructure (self.mesh) for computing descriptors.

• Computes statistics for equivalent diameter, aspect ratio, principal axes, and rotation axes when applicable.

• Can handle multiphase or single-phase microstructures.

Examples

>>> # Plot initial statistics with default settings
>>> rve.plot_stats_init()

>>> # Plot only the first phase (porous) and save figures
>>> rve.plot_stats_init(porous=True, save_files=True)

>>> # Compute descriptors and get figures and descriptor objects
>>> figs, descs = rve.plot_stats_init(get_res=True, return_descriptors=True)

>>> # Suppress console output and return figure objects
>>> figs = rve.plot_stats_init(silent=True)

plot_voxels(sliced=False, dual_phase=None, phases=False, cmap='prism', ori=None, color_key=0, silent=False)

Generate a 3D visualization of the voxelized RVE structure

This function visualizes the voxel-based microstructure of the RVE. It supports coloring by phase, grain ID, or crystallographic orientation, and can optionally render a sliced view of the 3D voxel mesh.

Parameters

slicedbool, optional

If True, generates a sliced view of the voxel mesh to visualize the internal structure. Default is False.

dual_phasebool or None, optional

Deprecated parameter for dual-phase visualization. Use phases instead. Default is None.

phasesbool, optional

If True, color voxels by phase instead of grain ID. Default is False.

cmapstr, optional

Name of the matplotlib colormap used for rendering. Default is ‘prism’.

oriarray-like, bool, or None, optional

Array of grain orientations, or True to use self.mesh.grain_ori_dict for coloring via inverse pole figure (IPF) mapping. Default is None.

color_keyint, optional

Selects the color mapping for orientations: - 0: iphHSVKey - 1: BungeColorKey - 2: ipfHKLKey Default is 0.

silentbool, optional

If True, suppresses figure display and returns the matplotlib figure object instead. Default is False.

Returns

figmatplotlib.figure.Figure or None

Returns the figure object if silent=True. Otherwise, displays the 3D plot and returns None.

Raises

ValueError

If self.mesh.grains is None, indicating that voxelization has not been performed.

Notes

• Requires that the voxel mesh (self.mesh) has been generated by voxelize().

• If ori is provided, orientation-based coloring is applied using get_ipf_colors().

• Prints a warning if dual_phase is used, since it is deprecated and replaced by phases.

• Automatically computes aspect ratios of the RVE to ensure accurate 3D visualization.

Examples

>>> # Simple 3D plot of voxelized RVE
>>> rve.plot_voxels()

>>> # Plot a sliced view of the voxel mesh
>>> rve.plot_voxels(sliced=True)

>>> # Color voxels by phase and use a custom colormap
>>> rve.plot_voxels(phases=True, cmap='viridis')

>>> # Use orientation-based coloring via IPF mapping
>>> rve.plot_voxels(ori=True, color_key=2)

>>> # Suppress figure display and get the matplotlib Figure object
>>> fig = rve.plot_voxels(silent=True)

smoothen(nodes_v=None, voxel_dict=None, grain_dict=None)

Generate smoothed grain boundaries from a voxelated mesh.

Parameters

nodes_varray-like or None, optional

Mesh node coordinates. If None, uses self.mesh.nodes.

voxel_dictdict or None, optional

Dictionary of voxels in the mesh. If None, uses self.mesh.voxel_dict.

grain_dictdict or None, optional

Dictionary mapping grains to their voxels. If None, uses self.mesh.grain_dict.

Returns

None

The smoothed nodes are stored in self.mesh.nodes_smooth. Grain boundary faces are optionally stored in self.geometry[‘GBfaces’].

Raises

ValueError

If nodes_v is None and self.mesh.nodes is not available.

AttributeError

If self.mesh is not initialized before calling smoothen().

Notes

• Requires self.mesh to be initialized by voxelize().

• Updates self.mesh.nodes_smooth with smoothed node coordinates.

• Adds ‘GBfaces’ entry to self.geometry if it exists.

voxelize(particles=None, dim=None)

Generate the RVE by assigning voxels to grains.

Parameters

particleslist or None, optional

List of particle objects to voxelize. If None, uses self.particles.

dimtuple of int, optional

3-tuple specifying the number of voxels in each spatial direction. If None, uses self.rve.dim.

Returns

None

The voxelized mesh is stored in self.mesh. Phase voxel fractions are stored in self.vf_vox and printed to the console.

Raises

ValueError

• If particles is None and self.particles is not available.

• If dim is not a 3-tuple when specified.

AttributeError

If self.rve or self.simbox is not initialized before voxelization.

Notes

• Requires self.particles to be initialized by pack().

• Updates self.mesh, self.ngrains, self.Ngr, and self.vf_vox.

• Logs warnings if phase volume fractions do not sum to 1.

• Removes polyhedral grain geometries (self.geometry) after re-meshing to avoid inconsistencies.

write_abq(nodes=None, file=None, path='./', voxel_dict=None, grain_dict=None, dual_phase=False, thermal=False, units=None, ialloy=None, nsdv=200, crystal_plasticity=False, phase_props=None, *, boundary_conditions: Dict[str, Any] | None = None)

Write the Abaqus input deck (.inp) for the generated RVE

This method generates an Abaqus input file for the current RVE. It supports voxelized or smoothened meshes, dual-phase materials, crystal plasticity, thermal analysis, custom material properties, and optional boundary conditions. Material definitions and mesh data are automatically handled based on provided arguments or class attributes.

Parameters

nodesstr or array-like, optional

Defines the mesh to write: - ‘voxels’, ‘v’ : use voxelized mesh - ‘smooth’, ‘s’ : use smoothened mesh - array-like : explicit nodal coordinates Default is None, automatically selecting available mesh.

filestr, optional

Filename for the Abaqus input deck. Default is auto-generated.

pathstr, optional

Directory path to save the input deck. Default is ‘./’.

voxel_dictdict, optional

Dictionary with voxel information. Default is self.mesh.voxel_dict.

grain_dictdict, optional

Dictionary mapping grain IDs to nodes. Default is self.mesh.grain_dict.

dual_phasebool, optional

If True, generate input for dual-phase materials. Default is False.

thermalbool, optional

If True, include thermal material definitions. Default is False.

unitsstr, optional

Units for the model, ‘mm’ or ‘um’. Default is self.rve.units.

ialloylist or object, optional

Material definitions for each phase. Default is self.rve.ialloy.

nsdvint, optional

Number of state variables per integration point for crystal plasticity. Default is 200.

crystal_plasticitybool, optional

If True, enable crystal plasticity material definitions. Default is False.

phase_propsdict, optional

Additional phase-specific material properties.

boundary_conditionsdict, optional

Dictionary specifying boundary conditions to write. Default is None.

Returns

filestr

Full path to the generated Abaqus input file.

Raises

ValueError

• If no voxelized or smoothened mesh is available when required.

• If invalid nodes argument is provided.

• If units are not ‘mm’ or ‘um’.

• If the list ialloy is longer than the number of phases in the RVE.

• If periodic boundary conditions are requested but the RVE is non-periodic.

Notes

• Automatically selects voxel or smoothened mesh if nodes is None.

• Handles dual-phase structures and crystal plasticity input.

• Writes additional material files if orientations are available and ialloy is provided.

• Visualization or mesh generation must be performed before calling this function.

Examples

>>> # Write voxelized RVE input deck with default settings
>>> abq_file = rve.write_abq(nodes='voxels')

>>> # Write smoothened RVE deck for dual-phase material
>>> abq_file = rve.write_abq(nodes='smooth', dual_phase=True, ialloy=alloy_list)

>>> # Include boundary conditions
>>> bc = {'ux': [0, 0.1], 'uy': [0, 0.1]}
>>> abq_file = rve.write_abq(nodes='voxels', boundary_conditions=bc)

write_abq_ori(ialloy=None, ori=None, file=None, path='./', nsdv=200)

Write Abaqus material input file using grain orientations for crystal plasticity

This function generates an Abaqus .inp file containing material definitions for crystal plasticity, using the provided grain orientations and material IDs. If ialloy or ori are not specified, the method uses the RVE’s default values.

Parameters

ialloylist or object, optional

Material identifiers for each phase. Default is self.rve.ialloy.

oridict or array-like, optional

Dictionary or array of grain orientations. Default is self.mesh.grain_ori_dict.

filestr, optional

Name of the output Abaqus material file. Default is auto-generated based on RVE name.

pathstr, optional

Directory path where the file will be saved. Default is ‘./’.

nsdvint, optional

Number of state variables per integration point for crystal plasticity. Default is 200.

Returns

filestr

Full path to the generated Abaqus material input file.

Raises

ValueError

• If ialloy is not provided and self.rve.ialloy is None.

• If ori is not provided and self.mesh.grain_ori_dict is None.

Notes

• Calls writeAbaqusMat internally to generate the material definitions.

• Assumes the RVE and grain orientations have been initialized prior to calling.

Examples

>>> # Write material file using default RVE orientations and material numbers
>>> abq_file = rve.write_abq_ori()

>>> # Specify custom material IDs and orientations
>>> abq_file = rve.write_abq_ori(ialloy=alloy_list, ori=ori_dict, file='custom_mat.inp')

write_centers(file=None, path='./', grains=None)

Write the center positions of grains to a CSV file

Parameters

filestr, optional

Filename for the CSV file. Default is auto-generated based on self.name.

pathstr, optional

Directory path to save the CSV file. Default is ‘./’.

grainsdict, optional

Dictionary of grain data. Default is self.geometry[‘Grains’].

Returns

None

Notes

• Each line in the CSV file corresponds to a grain center in the format: x, y, z.

• Polyhedral grains without simplices are skipped.

write_dataSchema(user_metadata: Dict[str, Any] | None = None, boundary_condition: Dict[str, Any] | None = None, phases: Dict[str, Any] | List[Dict[str, Any]] | None = None, interactive: bool = True, structured: bool = True, ialloy: int = 1, length_unit: str = 'µm') → dict

Generate a JSON-compatible data schema containing user, system, and job-specific elements

This function builds a comprehensive data dictionary for a microstructure simulation, including metadata, boundary conditions, phase information, voxel and grain data. It supports interactive prompts for missing information, structured/unstructured meshes, and unit scaling.

Parameters

user_metadatadict, optional

Prefilled metadata fields; required if interactive=False. Default is None.

boundary_conditiondict, optional

Dictionary specifying mechanical or thermal boundary conditions. Default is None.

phasesdict or list of dicts, optional

Phase-specific information; if None, default material library and ialloy are used.

interactivebool, optional

If True, prompt user for missing information. Default is True.

structuredbool, optional

Whether the mesh is structured. Default is True.

ialloyint, optional

Alloy index for selecting material properties from the built-in library. Default is 1.

length_unitstr, optional

Unit for length scaling; either ‘µm’ or ‘mm’. Default is ‘µm’.

Returns

dict

A nested dictionary containing the complete data schema for the simulation.

Raises

ValueError

If interactive=False and required metadata fields or boundary conditions are missing, or if length_unit is invalid

TypeError

If phases is not a dict or a list of dicts when provided

write_ori(angles=None, file=None, path='./')

Write grain orientations (Euler angles) to a CSV file

This method exports the orientations of grains in the microstructure. If no angles are provided, the method uses the stored grain orientations from the mesh. The CSV file contains one row per grain with three values representing the Euler angles (phi1, Phi, phi2).

Parameters

anglesarray-like of shape (N, 3), optional

Euler angles for each grain. If None, the stored orientations are used.

filestr, optional

Name of the output CSV file. If None, a default name based on the microstructure name and number of grains is used.

pathstr, optional

Directory path where the CSV file will be saved. Default is ‘./’.

Returns

str

Full path to the generated CSV file.

Raises

ValueError

If angles is None and no grain orientations are stored in self.mesh.grain_ori_dict.

Notes

• Each row in the CSV corresponds to one grain.

• Values are written in the order: phi1, Phi, phi2 (in radians).

Examples

>>> # Export stored orientations to default file
>>> rve.write_ori()

>>> # Export provided orientations to a specific file
>>> rve.write_ori(angles=my_angles, file='grain_orientations.csv', path='./data')

write_stl(data='grains', file=None, path='./', phases=False, phase_num=None)

Export grains or particles as STL files representing convex polyhedra

This function writes STL files with triangular facets for grains or particles. Each facet is written in standard STL ASCII format:

``` solid name

facet normal n1 n2 n3

outer loop

vertex p1x p1y p1z vertex p2x p2y p2z vertex p3x p3y p3z

endloop

endfacet

endsolid name ```

Parameters

data{‘grains’, ‘particles’}, optional

Determines whether to export grains or particles. Default is ‘grains’.

filestr, optional

Filename for the STL file. Default is generated from self.name.

pathstr, optional

Directory to save the STL file. Default is ‘./’.

phasesbool, optional

If True, export only grains of a specific phase. Default is False.

phase_numint, optional

Phase number to export if phases=True. Required in that case.

Returns

None

Raises

ValueError

• If phases=True but phase_num is not provided.

Notes

• Facet normals are automatically computed using cross products of vertices.

• Acute or irregular facets trigger warnings.

• For particle export, each particle must have a valid inner polyhedron.

Examples

>>> # Export all grains to STL
>>> rve.write_stl()

>>> # Export particles to STL
>>> rve.write_stl(data='particles')

>>> # Export only phase 1 grains
>>> rve.write_stl(phases=True, phase_num=1)

write_voxels(angles=None, script_name=None, file=None, path='./', mesh=True, source=None, system=False)

Write voxel structure of the microstructure to a JSON file

This function exports the voxel-based representation of the microstructure, including grain numbers, optional orientations, and mesh data. Metadata such as owner, system information, and script name are included.

Parameters

anglesnp.ndarray, optional

Array of Euler angles for grain orientations. If None, stored orientations are used if available. Default is None.

script_namestr, optional

Name of the script used to generate the microstructure. Default is the current script file.

filestr, optional

Name of the output JSON file. Default is based on microstructure name and number of grains.

pathstr, optional

Directory path to save the JSON file. Default is current directory ‘./’.

meshbool, optional

Whether to include mesh nodes and voxel connectivity in the output. Default is True.

sourceAny, optional

Optional input or source information to include in the JSON metadata.

systembool, optional

Whether to include system information in the JSON metadata. Default is False.

Returns

None

The function writes a JSON file and does not return any value.

Module GUI

A Graphical User Interface for create_rve.py, cuboid_grains.py and cpnvert_ang2rve.py Created on May 2024 last Update Oct 2024 @author: Ronak Shoghi, Alexander Hartmaier

kanapy.core.gui.add_label_and_entry(frame, row, label_text, entry_var, entry_type='entry', bold=False, options=None, col=0)

Add a label and an input widget (entry, checkbox, or combobox) to a given frame

Parameters

frametkinter.Frame

Parent frame where the widgets will be added

rowint

Row index in the frame grid layout

label_textstr or None

Text for the label; if None, no label is created

entry_vartkinter variable

Variable bound to the input widget (e.g., StringVar, BooleanVar)

entry_typestr, optional

Type of input widget: “entry”, “checkbox”, or “combobox” (default is “entry”)

boldbool, optional

Whether to display the label text in bold (default is False)

optionslist, optional

List of selectable options when entry_type is “combobox”

colint, optional

Column index for placing the label and entry in the grid (default is 0)

Returns

None

The function adds widgets directly to the frame

class kanapy.core.gui.cuboid_rve(app, notebook)

Bases: object

Class for managing RVEs with cuboid grains and associated GUI controls

Parameters

app: tk.Tk or tk.Frame

Reference to the main Tkinter application instance

notebook: ttk.Notebook

Reference to the parent notebook widget for GUI tab placement

Attributes

app: tk.Tk or tk.Frame

Reference to the main Tkinter application instance

canvas: tk.Canvas

Canvas for displaying the cuboid RVE

ms: object

Placeholder for the microstructure object

texture_var2: tk.StringVar

Selected texture type (default “random”)

matname_var2: tk.StringVar

Material name (default “Simulanium”)

ialloy: tk.IntVar

Number of alloys (default 2)

ngr_var: tk.StringVar

Number of grains in each direction (default “5, 5, 5”)

nv_gr_var: tk.StringVar

Number of voxels per grain in each direction (default “3, 3, 3”)

size_var2: tk.StringVar

RVE size in each direction (default “45, 45, 45”)

kernel_var2: tk.StringVar

Kernel parameter for unimodal textures (default “-” or “7.5”)

euler_var2: tk.StringVar

Euler angles for unimodal textures (default “-” or “0.0, 45.0, 0.0”)

Notes

The class handles creation, visualization, and parameter management for cuboid RVEs. GUI variable traces are used to automatically update dependent parameters such as kernel and Euler angle values based on the selected texture type.

close()

Quit and destroy the cuboid_rve GUI main window

Notes

This method terminates the Tkinter application and closes the main window

create_cubes_and_plot()

Create a microstructure object with cuboid grains and plot the RVE

Notes

Parses GUI parameters for number of grains, voxels per grain, and RVE size Initializes a Microstructure object and sets up the voxel mesh Assigns each cuboid grain an index and populates grain dictionaries Calls plot_voxels to generate the RVE figure and displays it on the GUI Returns nothing; updates the GUI canvas with the plotted RVE

create_orientation()

Create grain orientations for the cuboid RVE based on texture descriptors

Notes

Supports ‘unimodal’ textures with user-specified kernel and Euler angles Automatically generates the cuboid RVE if ms or ms.mesh is not initialized Calls generate_orientations to assign orientations to the microstructure Writes voxel data to a JSON file and plots the voxelized RVE with orientations Displays messages indicating progress and processing time

display_cuboid(fig)

Display the cuboid RVE figure on the GUI canvas

Parameters

figmatplotlib.figure.Figure

The figure object representing the cuboid RVE to display

Notes

Destroys any existing canvas before displaying the new figure Updates the Tkinter window geometry to fit the figure

export_abq()

Export the cuboid RVE mesh to an Abaqus input file

Notes

Automatically generates the cuboid RVE without orientations if ms is not initialized Calls write_abq to export the mesh in millimeter units Displays a progress message if RVE generation is required

update_euler_var(*args)

Update the Euler angles variable based on the current texture selection

Parameters

*argstuple

Optional arguments passed by the tkinter trace callback, not used directly

Notes

Sets euler_var2 to “0.0, 45.0, 0.0” if texture_var2 is ‘unimodal’, otherwise sets it to “-”

update_kernel_var(*args)

Update the kernel parameter variable based on the current texture selection

Parameters

*argstuple

Optional arguments passed by the tkinter trace callback, not used directly

Notes

Sets kernel_var2 to “7.5” if texture_var2 is ‘unimodal’, otherwise sets it to “-”

kanapy.core.gui.parse_entry(entry)

Convert a comma-separated string into a list of integers

Parameters

entrystr

String of comma-separated integer values

Returns

list of int

List of integers parsed from the input string

class kanapy.core.gui.particle_rve(app, notebook)

Bases: object

Class for generating Representative Volume Elements (RVEs) based on particle simulations first tab

This class defines the GUI logic and default parameters for building RVEs using particle-based microstructure simulations. It manages various parameters such as particle size distribution, aspect ratio, texture settings, and periodic boundary conditions.

Parameters

apptkinter.Tk or tkinter.Frame

Reference to the main Tkinter application instance.

notebookttk.Notebook

The notebook widget in which this tab (RVE setup) is placed.

Attributes

apptkinter.Tk or tkinter.Frame

Main application reference.

msobject or None

Placeholder for microstructure data.

ms_statsobject or None

Placeholder for microstructure statistical data.

ebsdobject or None

Placeholder for EBSD data (if used).

stats_canvas1tkinter.Canvas or None

Canvas for displaying statistical plots.

rve_canvas1tkinter.Canvas or None

Canvas for displaying the RVE visualization.

texture_var1tk.StringVar

Texture type, default “random”.

matname_var1tk.StringVar

Material name, default “Simulanium”.

nphasestk.IntVar

Number of material phases, default 1.

ialloytk.IntVar

Alloy type indicator, default 2.

nvox_var1tk.IntVar

Number of voxels per dimension in the RVE, default 30.

size_var1tk.IntVar

Physical size of the RVE, default 30.

periodic_var1tk.BooleanVar

Whether to apply periodic boundary conditions, default True.

volume_fractiontk.DoubleVar

Target total volume fraction, default 1.0.

vf_acttk.DoubleVar

Actual volume fraction, initialized to 0.0.

eq_diameter_sigtk.DoubleVar

Standard deviation of equivalent diameter distribution.

eq_diameter_scaletk.DoubleVar

Scale parameter for equivalent diameter distribution.

eq_diameter_loctk.DoubleVar

Location parameter for equivalent diameter distribution.

eq_diameter_mintk.DoubleVar

Minimum equivalent diameter.

eq_diameter_maxtk.DoubleVar

Maximum equivalent diameter.

eqd_act_sigtk.DoubleVar

Active (fitted or adjusted) standard deviation for equivalent diameter.

eqd_act_scaletk.DoubleVar

Active scale for equivalent diameter.

eqd_act_loctk.DoubleVar

Active location for equivalent diameter.

aspect_ratio_sigtk.DoubleVar

Standard deviation for aspect ratio distribution.

aspect_ratio_scaletk.DoubleVar

Scale parameter for aspect ratio distribution.

aspect_ratio_loctk.DoubleVar

Location parameter for aspect ratio distribution.

aspect_ratio_mintk.DoubleVar

Minimum aspect ratio.

aspect_ratio_maxtk.DoubleVar

Maximum aspect ratio.

ar_act_sigtk.DoubleVar

Active standard deviation for aspect ratio.

ar_act_scaletk.DoubleVar

Active scale for aspect ratio.

ar_act_loctk.DoubleVar

Active location for aspect ratio.

tilt_angle_kappatk.DoubleVar

Concentration parameter for tilt angle distribution.

tilt_angle_loctk.DoubleVar

Mean (location) of tilt angle distribution in radians.

tilt_angle_mintk.DoubleVar

Minimum tilt angle (0.0).

tilt_angle_maxtk.DoubleVar

Maximum tilt angle (π).

kernel_var1tk.StringVar

Orientation kernel width; depends on texture setting.

euler_var1tk.StringVar

Euler angles defining the texture orientation; depends on texture setting.

close()

Quit and destroy the particle_rve GUI main window

Notes

This method quits the Tkinter application and destroys the main window

create_and_plot_rve()

Create the RVE from current statistics and plot it along with associated statistics

Notes

Will overwrite existing ms_stats and ms objects Displays a progress message and measures processing time Initializes self.ms with the selected material and voxelizes the RVE Plots the voxelized RVE using plot_voxels and displays it on the GUI Updates activity-related variables based on voxelized statistics Also plots statistics figures returned from plot_stats_init

create_and_plot_stats()

Plot statistics of the current microstructure descriptors and initialize a new Microstructure object

Notes

Will erase the global microstructure object self.ms if it exists Reads current statistics using readout_stats Initializes self.ms with the selected material and texture Plots statistics using plot_stats_init and displays each figure on the GUI Resets activity-related variables after plotting

create_orientation()

Generate grain orientations based on the selected texture and assign them to the RVE

Notes

Supports ‘unimodal’ textures with user-specified kernel and Euler angles, or ‘EBSD-ODF’ textures Automatically generates the RVE if ms_stats or ms objects are not initialized Calls generate_orientations to assign orientations to the microstructure Writes voxel data to a JSON file and plots the voxelized RVE with orientations Displays messages indicating progress and processing time

display_plot(fig, plot_type)

Show a statistics graph or RVE plot on the GUI canvas

Parameters

figmatplotlib.figure.Figure

The figure object to be displayed

plot_typestr

Type of plot to display, either ‘stats’ for statistics graph or ‘rve’ for RVE plot

Notes

Existing canvas for the specified plot type will be destroyed before displaying the new figure The GUI window size is updated to fit the new plot

export_abq()

Export the RVE mesh to an Abaqus input file

Notes

If ms_stats, ms, or ms.mesh is not initialized, the RVE is first generated without orientations Checks if the material is dual-phase based on volume fraction Calls write_abq to export the mesh in millimeter units Displays a progress message if RVE generation is required

extract_microstructure_params()

Extract microstructure parameters from the EBSD data and update GUI variables

Notes

If self.ebsd is None, the method does nothing Extracts grain size, aspect ratio, and orientation parameters from the first EBSD dataset Updates GUI variables for material name, volume fraction, equivalent diameter, aspect ratio, tilt angle, and texture type Computed min and max cutoff values are based on statistical scaling of the extracted parameters

import_ebsd()

Import an EBSD map and extract microstructure parameters

Notes

Opens a file dialog to select an EBSD map with extensions ‘.ctf’ or ‘.ang’ Displays messages indicating progress and success or failure Calls extract_microstructure_params and reset_act after successful import

import_stats()

Import statistical data from a JSON file and update GUI variables

Notes

Opens a file dialog to select a statistics file with ‘.json’ extension Updates GUI variables for material name, RVE size, voxel counts, periodicity, volume fraction, equivalent diameter, aspect ratio, and tilt angle based on imported data Calls reset_act and clears ebsd after successful import Displays a message indicating success or failure

readout_stats()

Collect and return the current microstructure and RVE statistics

Returns

dict

A dictionary containing: - ‘Grain type’: Type of grain - ‘Equivalent diameter’: Distribution parameters (sig, scale, loc, cutoff_min, cutoff_max) - ‘Aspect ratio’: Distribution parameters (sig, scale, loc, cutoff_min, cutoff_max) - ‘Tilt angle’: Orientation parameters (kappa, loc, cutoff_min, cutoff_max) - ‘RVE’: RVE size and voxel counts - ‘Simulation’: Simulation settings including periodicity and output units - ‘Phase’: Material phase information including name, number, and volume fraction

reset_act()

Reset all activity-related variables to zero

Notes

Sets vf_act, eqd_act_sig, eqd_act_scale, ar_act_sig, and ar_act_scale to 0.0

update_euler_var(*args)

Update the Euler angles variable based on the current texture selection

Parameters

*argstuple

Optional arguments passed by the tkinter trace callback, not used directly

Notes

If self.texture_var1 is ‘unimodal’, self.euler_var1 is set to “0.0, 45.0, 0.0” Otherwise, self.euler_var1 is set to “-”

update_kernel_var(*args)

Update the kernel variable based on the current texture selection

Parameters

*argstuple

Optional arguments passed by the tkinter trace callback, not used directly

Notes

If self.texture_var1 is ‘unimodal’, self.kernel_var1 is set to “7.5” Otherwise, self.kernel_var1 is set to “-”

write_stat_param()

Save the current microstructure statistics to a file

Notes

If self.ms_stats is None, a message is shown indicating no stats are available Opens a file dialog to select the save location Calls write_stats to write the statistics to the selected file

kanapy.core.gui.self_closing_message(message, duration=4000)

Display a temporary popup message box that closes automatically after a given duration

Parameters

messagestr

The message text to display in the popup window

durationint, optional

Time in milliseconds before the message box closes automatically (default is 4000)

Returns

None

The function creates and destroys a popup window; no value is returned

Module CLI

kanapy.core.cli.chkVersion(matlab)

Read the installed MATLAB version from a version string

Parses the given MATLAB version string to extract the release year (e.g., ‘R2023a’ → 2023). If the version cannot be determined, returns None.

Parameters

matlabstr

String containing MATLAB version information

Returns

int or None

MATLAB release year if successfully parsed, otherwise None

kanapy.core.cli.setPaths()

Start the MATLAB engine and initialize the MTEX environment

Checks if the MATLAB engine for Python is installed and installs it if missing. Then initializes the MATLAB engine and MTEX toolbox for use with Kanapy.

Raises

ModuleNotFoundError

If kanapy-mtex or MATLAB are not installed, or if the MATLAB engine installation fails

Notes

• Requires MATLAB 2025a or later

• Automatically installs the matlabengine package if not found

• Configures Kanapy for texture analysis by running init_engine.py

kanapy.core.cli.start()

Module initialization

Classes for RVE and mesh initialization

Authors: Mahesh Prassad, Abhishek Biswas, Alexander Hartmaier Ruhr University Bochum, Germany

March 2024

class kanapy.core.initializations.NodeSets(nodes)

Bases: object

Identify nodes on faces of a cuboidal mesh and store them in face-specific sets

Parameters

nodesndarray

Array of nodal coordinates of shape (n_nodes, 3)

Attributes

F0yz, F0yz_fulllist of int

Nodes on left face

F1yz, F1yz_fulllist of int

Nodes on right face

Fx0z, Fx0z_fulllist of int

Nodes on bottom face

Fx1z, Fx1z_fulllist of int

Nodes on top face

Fxy0, Fxy0_fulllist of int

Nodes on rear face

Fxy1, Fxy1_fulllist of int

Nodes on front face

surfSetlist of int

All nodes on any face

Notes

• Uses np.isclose to identify nodes lying on the boundaries

• Each *_full list keeps a copy of the original face node indices

• surfSet includes all nodes belonging to any face

CreatePeriodicEdgeSets(Nodes, sortCoord, NodeSet)

Create a sorted list of nodes along an edge to facilitate periodic boundary conditions

Parameters

Nodeslist of int

List of all node indices in the mesh

sortCoordlist or ndarray

Coordinates of nodes along the sorting direction

NodeSetlist of int

Node indices on the edge to be sorted

Returns

sortedListlist of int

Node indices sorted according to sortCoord

CreatePeriodicNodeSets(Nodes, sortCoord1, sortCoord2, NodeSet)

Create a sorted list of nodes for a surface to facilitate periodic boundary conditions

Parameters

Nodeslist of int

List of all node indices in the mesh

sortCoord1list or ndarray

Coordinates of nodes along the first sorting direction

sortCoord2list or ndarray

Coordinates of nodes along the second sorting direction

NodeSetlist of int

Node indices on a surface to be sorted

Returns

sortedListlist of int

Node indices sorted according to sortCoord1 and sortCoord2

RemoveItemInList(NodeList, ReplaceNodeList)

Remove a set of nodes from a list of nodes

Parameters

NodeListlist of int

Original list of node indices

ReplaceNodeListlist of int

Node indices to be removed from NodeList

Returns

NodeListlist of int

Updated list after removing the specified nodes

class kanapy.core.initializations.RVE_creator(stats_dicts, nsteps=1000, from_voxels=False, poly=None)

Bases: object

Creates an RVE based on user-defined statistics

Generates ellipsoid size distribution (Log-normal) based on user-defined statistics. Particle, RVE and simulation data are written as JSON files in a folder in the current working directory for later access.

Parameters

stats_dictslist of dict

List of dictionaries containing microstructure descriptors for each phase

nstepsint, optional

Maximum number of steps for packing simulation (default is 1000)

from_voxelsbool, optional

If True, RVE is created from voxel input (default is False)

polyobject, optional

Optional polygon object for particle generation

Attributes

packing_stepsint

Max number of steps for packing simulation

sizetuple of float

Side lengths of the RVE along Cartesian axes

dimtuple of int

Number of voxels along Cartesian axes

periodicbool

Whether the RVE is periodic

unitsstr

Units of RVE dimensions, either “mm” or “um”

nparticleslist of int

Number of particles for each phase

particle_datalist of dict

Statistical particle data for each phase

phase_nameslist of str

Names of phases

phase_vflist of float

Volume fractions of each phase

ialloylist of int

Alloy numbers for ICAMS CP-UMAT

Notes

1. Input parameters provided by the user in the input file are: - Standard deviation for ellipsoid equivalent diameter (Log-normal or Normal distribution) - Mean value of ellipsoid equivalent diameter (Log-normal or Normal distribution) - Minimum and Maximum cut-offs for ellipsoid equivalent diameters - Mean value for aspect ratio - Mean value for ellipsoid tilt angles (Normal distribution) - Side dimension of the RVE - Discretization along the RVE sides

2. Data written in output files include: - Ellipsoid attributes: Major, Minor, Equivalent diameters and tilt angle - RVE attributes: size, number of voxels, voxel resolution - Simulation attributes: periodicity and output unit scale (mm or μm) for ABAQUS .inp file

class kanapy.core.initializations.mesh_creator(dim)

Bases: object

Create a mesh object for voxel-based microstructure representation

Parameters

dimtuple of int

3-tuple representing the number of voxels along each Cartesian direction

Attributes

dimtuple of int

Dimension tuple: number of voxels in each Cartesian direction

nvoxint

Total number of voxels

phasesndarray

Field data storing phase numbers for each voxel

grainsndarray

Field data storing grain numbers for each voxel

voxel_dictdict

Dictionary mapping voxel number to associated nodes

grain_dictdict

Dictionary mapping grain number to associated voxels

grain_phase_dictdict

Dictionary storing phase per grain

grain_ori_dictdict

Dictionary storing orientation per grain

vox_center_dictdict

Dictionary storing center coordinates of each voxel

nodesndarray

Array of nodal positions

nodes_smoothndarray

Array of nodal positions after smoothing grain boundaries

prec_vf_voxelsfloat

Actual volume fraction of precipitates in voxelated structure

Notes

• Raises ValueError if dim is not a 3-tuple

• Initializes data structures to store mesh, grains, phases, and nodes

• voxel_dict is initialized as defaultdict(list) to store node lists per voxel

create_voxels(sim_box)

Generate voxels and nodes inside the defined RVE (simulation box)

Parameters

sim_boxentities.Cuboid

Simulation box object representing the RVE dimensions

Returns

None

Populates the mesh_creator object with: - nodes : ndarray

Array of nodal coordinates

• voxel_dictdict

  Dictionary mapping voxel ID to list of node IDs

• vox_center_dictdict

  Dictionary mapping voxel ID to center coordinates

Notes

• Nodes are generated along Cartesian axes with spacing defined by dim

• Voxel centers are computed as midpoint of voxel corners

• 8-node hexahedral (C3D8) element connectivity is maintained

• Duplicate nodes are avoided using verticesDict

get_ind(addr)

Convert a voxel address to a flat array index

Parameters

addrint or tuple of int

Address of the voxel. Can be a single integer index or a 3-tuple (i, j, k) representing voxel coordinates along each Cartesian axis

Returns

indint or None

Flattened array index corresponding to the voxel address. Returns None if addr is None, returns addr unchanged if addr is an empty list

Notes

• Assumes row-major ordering: index = i*dim[1]*dim[2] + j*dim[1] + k

• Raises ValueError if addr is not a single integer or a 3-tuple

kanapy.core.initializations.set_stats(grains, ar=None, omega=None, deq_min=None, deq_max=None, asp_min=None, asp_max=None, omega_min=None, omega_max=None, size=100, voxels=60, gtype='Elongated', rveunit='um', periodicity=False, VF=None, phasename=None, phasenum=None, save_file=False)

Create a dictionary containing statistical grain and RVE information

Parameters

grainslist of float

Parameters [sigma, loc, scale] of lognormal distribution for equivalent diameter

arlist of float, optional

Parameters [sigma, loc, scale] of lognormal distribution for aspect ratio (required for Elongated grains)

omegalist of float, optional

Parameters [kappa, loc] of von Mises distribution for tilt angle (required for Elongated grains)

deq_min, deq_maxfloat, optional

Minimum and maximum cutoff for equivalent diameter

asp_min, asp_maxfloat, optional

Minimum and maximum cutoff for aspect ratio

omega_min, omega_maxfloat, optional

Minimum and maximum cutoff for tilt angle

sizeint, optional

Side length of cubic RVE

voxelsint, optional

Number of voxels per side of RVE

gtypestr, optional

Grain type, either ‘Elongated’ or ‘Equiaxed’

rveunitstr, optional

Unit of RVE dimensions (‘um’ or ‘mm’)

periodicitybool or str, optional

Whether RVE is periodic

VFfloat, optional

Volume fraction of phase

phasenamestr, optional

Name of phase

phasenumint, optional

Phase number

save_filebool, optional

If True, save the dictionary as JSON

Returns

ms_statsdict

Dictionary containing statistical grain data, RVE info, simulation settings, and phase info

Notes

• Checks consistency of grain type and required parameters

• Sets default cutoff values if not provided

• Supports saving statistical info to JSON

kanapy.core.initializations.stat_names(legacy=False)

Return standardized names for statistical descriptors

Parameters

legacybool, optional

If True, use legacy naming convention (‘std’, ‘offs’, ‘mean’, ‘kappa’); otherwise, use current naming convention (‘sig’, ‘loc’, ‘scale’, ‘kappa’).

Returns

sigstr

Name for the standard deviation descriptor

locstr

Name for the location descriptor

scalestr

Name for the scale/mean descriptor

kappastr

Name for the kappa/shape parameter

Module input_output

kanapy.core.input_output.export2abaqus(nodes, file, grain_dict, voxel_dict, units: str = 'um', gb_area=None, dual_phase=False, thermal=False, ialloy=None, grain_phase_dict=None, crystal_plasticity=False, phase_props=None, *, boundary_conditions: Dict[str, Any] | None = None)

Create an ABAQUS input file with microstructure morphology information including nodes, elements, and element sets

Parameters

nodeslist

List of node objects or coordinates

filestr

Output file path for the ABAQUS input file

grain_dictdict

Dictionary containing grain information

voxel_dictdict

Dictionary containing voxel-to-grain mapping

unitsstr, optional

Units used in the input file (default is ‘um’)

gb_areaoptional

Grain boundary area information

dual_phasebool, optional

If True, element sets with phase numbers are defined and assigned to materials “PHASE_{phase_id}MAT” If False, each grain refers to a material “GRAIN_{grain_id}MAT”

thermalbool, optional

If True, thermal properties are included

ialloyoptional

Alloy information for grains, used if dual_phase is False

grain_phase_dictdict, optional

Mapping from grain ID to phase ID

crystal_plasticitybool, optional

If True, crystal plasticity data is included

phase_propsoptional

Phase properties for crystal plasticity

boundary_conditionsdict, optional

Dictionary defining boundary conditions, keys may include type, loading_direction, value, etc.

Notes

If dual_phase is False, a “_mat.inp” file with the same name is expected to define alloy number and Euler angles for each grain. Element sets are written for grains or phases depending on dual_phase. The function handles nodes, elements, sets, and optionally boundary conditions for ABAQUS simulations.

kanapy.core.input_output.import_stats(file, path='./')

Read microstructure statistical descriptors from a JSON file.

This function loads and parses a JSON file containing statistical information about a microstructure, such as RVE dimensions, phase fractions, or grain statistics.

Parameters

filestr

Filename of the JSON file to read. The ‘.json’ extension will be appended automatically if missing.

pathstr, optional

Directory path where the JSON file is located (default: ‘./’).

Returns

descdict

Dictionary containing the statistical microstructure descriptors.

Raises

ValueError

If file is None.

FileNotFoundError

If the specified JSON file does not exist.

json.JSONDecodeError

If the file cannot be parsed as valid JSON.

OSError

If the file cannot be read due to permission or I/O errors.

Notes

• The function expects the JSON file to contain key-value pairs describing microstructure statistics compatible with the output of write_stats().

Examples

>>> desc = import_stats("example_stats.json")
>>> print(desc["RVE"]["Nx"])
20

kanapy.core.input_output.import_voxels(file, path='./')

Import a voxelized microstructure from a JSON file and reconstruct a Microstructure object for further analysis or simulation.

The voxel file typically contains: - Grain-wise orientation, phase, and shape information - Global model metadata (size, periodicity, phase names, etc.) - Optionally, mesh node coordinates and voxel connectivity

Parameters

filestr

Filename of the voxelized microstructure JSON file to import.

pathstr, optional

Path where the JSON file is located (default: ‘./’).

Returns

msMicrostructure

Fully reconstructed microstructure object containing: - Grain geometry, phases, orientations - Voxel-level mesh and connectivity - Simulation box and RVE setup - Volume fractions and statistics

Raises

ValueError

If file is None.

FileNotFoundError

If the specified voxel file cannot be found.

KeyError

If required keys (e.g. ‘Data’, ‘Model’) are missing in the JSON file.

json.JSONDecodeError

If the file is not a valid JSON.

RuntimeError

If the phase volume fractions do not sum to 1.0 (severe data inconsistency).

Notes

• If grain_phase_dict or orientation information is missing, the function will fall back to single-phase mode and log warnings.

• The mesh is either reconstructed from the JSON (if provided) or generated using mesh_creator().

• Periodicity and unit information are retained from the model metadata.

Examples

>>> ms = import_voxels('example_vox.json', path='./input')
>>> print(ms.Ngr, 'grains loaded with', ms.nphases, 'phases.')
>>> print(ms.mesh.nodes.shape, 'mesh nodes')

kanapy.core.input_output.pickle2microstructure(file, path='./')

Load a pickled microstructure object from disk.

Parameters

filestr

Filename of the pickled microstructure.

pathstr, optional

Directory where the pickle file is stored (default: ‘./’).

Returns

pclMaterial

Unpickled microstructure object.

Raises

ValueError

If file is None.

FileNotFoundError

If the specified pickle file does not exist.

pickle.UnpicklingError

If the file cannot be unpickled (e.g., corrupted or invalid format).

kanapy.core.input_output.read_dump(file)

Read a .dump file to extract simulation box and ellipsoid information for voxelization

Parameters

filestr

Path to the .dump file containing ellipsoid data generated in the packing routine

Returns

sim_boxCuboid

Cuboid object representing the RVE (simulation box)

Ellipsoidslist of Ellipsoid

List of ellipsoid objects representing the grains

Raises

FileNotFoundError

If the specified .dump file does not exist

Notes

The function reads the simulation box dimensions and ellipsoid attributes including position, axes lengths, orientation, and phase number. Duplicate ellipsoids are identified based on naming convention in the dump file

kanapy.core.input_output.writeAbaqusMat(ialloy, angles, file=None, path='./', grain_phase_dict=None, nsdv=200)

Export Euler angles to Abaqus input deck that can be included in the _geom.inp file. If parameter “grain_phase_dict” is given, the phase number for each grain will be used to select the corresponding ialloy from a list. If the list ialloy is shorter than the number of phases in grain_phase_dict, no angles for phases with no corresponding ialloy will be written.

Parameters:

ialloyint or list

Identifier, alloy number in ICAMS CP-UMAT: mod_alloys.f

anglesdict or (N, 3)-ndarray

Dict with Euler angles for each grain or array with number of N rows (= number of grains) and

three columns phi1, Phi, phi2

filestr

Filename, optional (default: None)

pathstr

Path to save file, option (default: ‘./’)

grain_phase_dict: dict

Dict with phase for each grain, optional (default: None)

nsdvint

Number of state dependant variables, optional (default: 200)

kanapy.core.input_output.write_dump(Ellipsoids, sim_box)

Write .dump files into a sub-directory “dump_files” for visualization or reuse in Kanapy

Parameters

Ellipsoidslist

Contains information of ellipsoids such as positions, axes lengths, and tilt angles

sim_boxCuboid

Contains information of the dimensions of the simulation box

Returns

None

Notes

The function creates a ‘dump_files’ directory in the current working directory if it does not exist and writes a file named ‘particle.<timestep>.dump’, where <timestep> is given by sim_box.sim_ts. The generated .dump files can be read by visualization software like OVITO or imported back into Kanapy to avoid repeating the packing simulation. Each file contains simulation domain bounds and ellipsoid attributes including position, axes lengths, and quaternion orientation.

kanapy.core.input_output.write_stats(stats, file, path='./')

Write microstructure statistical descriptors to a JSON file.

This function serializes the provided statistical data (e.g., phase fractions, grain sizes, RVE dimensions) and writes it to disk in JSON format. The .json extension is automatically appended if not provided.

Parameters

statsdict

Dictionary containing statistical descriptors of the microstructure (e.g., grain count, phase fractions, RVE size, or any other metadata).

filestr

Output filename for the JSON file. The ‘.json’ extension will be appended automatically if missing.

pathstr, optional

Directory path where the JSON file will be written (default: ‘./’).

Raises

ValueError

If stats or file is None.

OSError

If the file cannot be written (e.g., due to permission or path issues).

TypeError

If stats contains non-serializable objects (invalid for JSON encoding).

Notes

• The function uses Python’s built-in json module.

• The output file is overwritten if it already exists.

Examples

>>> stats = {"RVE": {"Nx": 20, "Ny": 20, "Nz": 20}, "Phase": {"Volume fraction": 0.8}}
>>> write_stats(stats, "example_stats")
# Writes './example_stats.json'

Module packing

kanapy.core.packing.calculateForce(Ellipsoids, sim_box, periodicity, k_rep=0.0, k_att=0.0)

Calculate the interaction forces between ellipsoids within the simulation box

Computes pairwise repulsive or attractive forces based on distance and phase between ellipsoids. Applies periodic boundary conditions if enabled.

Parameters

Ellipsoidslist of Ellipsoid

List of ellipsoid instances for which forces are calculated

sim_boxSimulation_Box

Simulation box representing the RVE dimensions

periodicitybool

If True, applies periodic boundary conditions

k_repfloat, optional

Repulsion factor for particles of the same phase (default is 0.0)

k_attfloat, optional

Attraction factor for particles of different phases (default is 0.0)

kanapy.core.packing.packingRoutine(particle_data, periodic, nsteps, sim_box, k_rep=0.0, k_att=0.0, fill_factor=None, poly=None, save_files=False, verbose=False)

Perform particle packing routine using particle generation and growth simulation

The function first generates ellipsoids from the provided particle statistics and then grows them over time steps while handling collisions and interactions. Uses particle_generator() to create particles and particle_grow() to grow and settle them.

Parameters

particle_datalist of dict

Statistics describing particle attributes for generation

periodicbool

Flag indicating if periodic boundary conditions are applied

nstepsint

Total number of timesteps for the growth simulation

sim_boxSimulation_Box

Simulation box representing the RVE dimensions

k_repfloat, optional

Repulsion factor for same-phase particles (default 0.0)

k_attfloat, optional

Attraction factor for different-phase particles (default 0.0)

fill_factorfloat, optional

Target volume fraction for particle filling (default None, uses 0.65)

polyndarray, optional

Points defining a primitive polygon inside ellipsoids (default None)

save_filesbool, optional

Whether to save dump files during simulation (default False)

verbosebool, optional

If True, prints detailed simulation output (default False)

Returns

particleslist

List of generated and packed ellipsoids

simboxSimulation_Box

Updated simulation box with current timestep information

Notes

Particle, RVE, and simulation data are read from JSON files generated by kanapy.input_output.particleStatGenerator(). These files contain:

• Ellipsoid attributes such as Major, Minor, Equivalent diameters, and tilt angles

• RVE attributes such as simulation domain size, number of voxels, and voxel resolution

• Simulation attributes such as total number of timesteps and periodicity

kanapy.core.packing.particle_generator(particle_data, sim_box, poly)

Initialize a list of ellipsoids by assigning random positions, orientations, and sizes within the given simulation box.

Parameters

particle_datadict

Dictionary containing ellipsoid properties such as major, minor, and equivalent diameters, tilt angles, and number of particles per phase.

sim_boxentities.Simulation_Box

Simulation box object defining the representative volume element (RVE) dimensions (width, height, depth).

polyndarray of shape (N, 3), optional

Points defining a primitive polygon inside the ellipsoid. Used for geometry construction.

Returns

list

List of Ellipsoid objects initialized for the packing routine.

Notes

The function introduces a scaling factor (0.5) to reduce overlap among generated ellipsoids. Ellipsoids are assigned random colors and positions within the simulation box.

kanapy.core.packing.particle_grow(sim_box, Ellipsoids, periodicity, nsteps, k_rep=0.0, k_att=0.0, fill_factor=None, dump=False, verbose=False)

Perform recursive particle growth and collision detection within the simulation box. Initializes an entities.Octree instance and progressively grows ellipsoids while handling inter-particle and wall collisions.

Parameters

sim_boxentities.Simulation_Box

Simulation box representing the representative volume element (RVE).

Ellipsoidslist

List of Ellipsoid objects used in the packing routine.

periodicitybool

Whether periodic boundary conditions are applied.

nstepsint

Total number of simulation steps for filling the box with particles.

k_repfloat, optional

Repulsion factor for particle interactions (default: 0.0).

k_attfloat, optional

Attraction factor for particle interactions (default: 0.0).

fill_factorfloat, optional

Target volume fraction for particle filling (default: 0.65).

dumpbool, optional

If True, dump files for particles are written at intervals (default: False).

verbosebool, optional

If True, print detailed information at iteration steps (default: False).

Returns

Ellipsoidslist

Updated list of Ellipsoid objects after particle growth.

sim_boxentities.Simulation_Box

Updated simulation box object after the packing process.

Notes

The function calls kanapy.input_output.write_dump() at each time step to write .dump files. Periodic images are written by default but can be disabled inside that function.

Module entities

class kanapy.core.entities.Cuboid(left, top, right, bottom, front, back)

Bases: object

Create Cuboid objects for ellipsoids and Octree sub-branches

Parameters

leftfloat

Bounding box minimum along x

topfloat

Bounding box minimum along y

rightfloat

Bounding box maximum along x

bottomfloat

Bounding box maximum along y

frontfloat

Bounding box minimum along z

backfloat

Bounding box maximum along z

intersect(other)

Evaluate whether the Cuboid object of the ellipsoid intersects with the Cuboid object of the Octree sub-branch

Parameters

other: Cuboid

Sub-branch cuboid object of the octree

Returns

bool

True if intersection occurs, False otherwise

class kanapy.core.entities.Ellipsoid(iden, x, y, z, a, b, c, quat, phasenum=0, dup=None, points=None)

Bases: object

Creates Ellipsoid objects for each ellipsoid generated from input statistics

Parameters

idenint

ID of the ellipsoid

xfloat

X-coordinate of the ellipsoid center

yfloat

Y-coordinate of the ellipsoid center

zfloat

Z-coordinate of the ellipsoid center

afloat

Semi-major axis length of the ellipsoid

bfloat

Semi-minor axis length of the ellipsoid

cfloat

Semi-minor axis length of the ellipsoid

quatnumpy.ndarray

Quaternion representing the ellipsoid’s orientation

phasenumint, optional

Phase number of the ellipsoid, default is 0

dupoptional

Duplicate status used for voxelization, default is None

pointslist or None, optional

Points used to create a Delaunay tessellation for the ellipsoid, default is None

Attributes

idint

ID of the ellipsoid

x, y, zfloat

Position of the ellipsoid center

xold, yold, zoldfloat

Previous positions

a, b, cfloat

Semi-major and semi-minor axes lengths

oria, orib, oricfloat

Original axes lengths

speedx, speedy, speedzfloat

Velocity components, initialized to 0

force_x, force_y, force_zfloat

Forces acting on the ellipsoid, initialized to 0

rotation_matrixndarray

Rotation matrix of the ellipsoid

surface_pointslist

Surface points of the ellipsoid

inside_voxelslist

Voxels belonging to the ellipsoid

duplicateoptional

Duplicate status used for voxelization

phasenumint

Phase number

brancheslist

Branches associated with the ellipsoid

neighborlistset

Neighbor ellipsoids

ncollisionint

Number of collisions

inneroptional

Delaunay tessellation of points if provided, else None

Notes

1. The orientation of each ellipsoid in the global coordinate space is defined by its tilt angle and axis vector, expressed in quaternion notation.

2. Ellipsoids are initialized without a velocity; a random value is later assigned by kanapy.packing.particle_generator.

3. An empty list for storing voxels belonging to the ellipsoid is initialized.

Bbox()

Compute the axis-aligned bounding box of the ellipsoid using its surface points

Sets the attributes: - bbox_xmin, bbox_xmax - bbox_ymin, bbox_ymax - bbox_zmin, bbox_zmax

create_poly(points)

Create a polygon inside the ellipsoid

This method applies a rotation to the input points using the object’s rotation_matrix and computes the Delaunay triangulation to form a polygon

Parameters

pointsarray_like

Input points to construct the polygon

Returns

Delaunay

A Delaunay triangulation object representing the polygon

get_coeffs()

Return the semi-axes coefficients of the ellipsoid

Returns

numpy.ndarray

A 1D array [a, b, c] representing the semi-major and semi-minor axes lengths of the ellipsoid.

get_cub()

Return the cuboid object of the ellipsoid

Returns

Cuboid

Cuboid object representing the ellipsoid’s bounding cuboid

get_pos()

Return the current position of the ellipsoid

Returns

numpy.ndarray

A 1D array [x, y, z] representing the current center coordinates of the ellipsoid.

get_volume()

Return the volume of the ellipsoid

Returns

float

The volume of the ellipsoid calculated as (4/3) * pi * a * b * c.

gravity_effect(value)

Move the ellipsoid downwards to mimic the effect of gravity acting on it

Parameters

valuefloat

User defined value for downward movement

Notes

The Cuboid object of the ellipsoid must be updated every time it moves

growth(fac)

Increase the size of the ellipsoid along its axes by a scaling factor

Parameters

facfloat

Scaling factor applied to the original axes lengths.

move(dt)

Move the ellipsoid by updating its position vector using the Verlet integration method

This method updates the ellipsoid’s position and velocity components based on the current force and previous positions, and then updates the Cuboid object.

Parameters

dtfloat

Time step used in the Verlet integration

Notes

The Cuboid object of the ellipsoid must be updated every time the ellipsoid moves

rotationMatrixGen()

Compute the rotation matrix of the ellipsoid from its quaternion

Returns

numpy.ndarray

A 3x3 rotation matrix representing the ellipsoid’s orientation.

set_cub()

Initialize an object of the class Cuboid using the bounding box limits from Bbox

This method calls the Bbox method to obtain the bounding box limits and then creates a Cuboid object using these limits

surfacePointsGen(nang=20)

Generate points on the outer surface of the ellipsoid using its rotation matrix

Parameters

nangint, optional

Number of points along each angular direction (default is 20).

Returns

numpy.ndarray

An array of shape (nang*nang, 3) containing 3D coordinates of points on the ellipsoid surface.

sync_poly(scale=None)

Move the center of the polygon to the center of the ellipsoid and scale the hull to fit inside the ellipsoid

This method recenters the polygon points at the ellipsoid’s center, applies rotation and scaling to fit the polygon inside the ellipsoid, and updates the Delaunay triangulation.

Parameters

scalefloat, optional

Scaling factor to apply to the polygon. If None, the default poly_scale from kanapy is used.

Notes

The function assumes that self.inner contains a Delaunay object representing the polygon. If self.inner is None, the method does nothing.

wallCollision(sim_box, periodicity)

Evaluate whether the ellipsoid collides with the boundaries of the simulation box

This method checks if the ellipsoid intersects with the simulation box walls. If periodicity is enabled, duplicates of the ellipsoid are created on opposite faces. If periodicity is disabled, the ellipsoid bounces back from the walls.

Parameters

sim_boxSimulation_Box

Simulation box object containing boundary limits

periodicitybool

Status of periodicity

Returns

list

List of ellipsoid duplicates if periodicity is enabled, otherwise an empty list

Notes

The Cuboid object of the ellipsoid must be updated every time the ellipsoid moves

class kanapy.core.entities.Octree(level, cub, particles=[])

Bases: object

Create an Octree object for tree trunk and its sub-branches

Parameters

level: int

Current level of the Octree, 0 for the trunk

cub: Cuboid

Cuboid object of the tree trunk or sub-branches, should be entire simulation box for the trunk

particles: list

List of particles within the tree trunk or sub-branches, contains all ellipsoids in the simulation domain for the trunk

Notes

1. level is set to zero for the trunk of the Octree

2. cub should be entire simulation box for the tree trunk

3. particles list contains all the ellipsoids in the simulation domain for the tree trunk

add_particle(particle)

Update the particle list of the Octree sub-branch

Parameters

particle: object

Particle object to be added to the sub-branch

collisionsTest()

Test for collisions between all ellipsoids in the Octree sub-branch

Returns

int

Number of collisions detected

Notes

Uses bounding sphere check as a preliminary filter and then calls the collision_routine to determine actual overlaps. Updates the collision count for each ellipsoid

get_cub()

Return the cuboid object of the octree sub-branch

Returns

Cuboid

Cuboid object corresponding to the octree sub-branch

make_neighborlist()

Find the neighbor list for each particle in the Octree sub-branch

Notes

Initializes the neighborlist of each particle as a set and updates it with particles from all branches that the particle belongs to

subdivide()

Divide the Octree sub-branch into eight further sub-branches and initialize each as an Octree object

Notes

Each newly created sub-branch is appended to the branches list of the current Octree

subdivide_particles()

Evaluate which ellipsoids belong to each Octree sub-branch by checking intersections

Notes

Calls the intersect method of each sub-branch cuboid with each particle cuboid and adds the particle to the sub-branch if an intersection occurs

update()

Update the Octree and begin recursive subdivision or particle assignment

Notes

If the number of particles exceeds the maximum allowed and the current level is below the maximum, the sub-branch is subdivided and particles are distributed among the new branches. Otherwise, particles are associated with this branch

class kanapy.core.entities.Simulation_Box(size)

Bases: object

Represents a 3D simulation domain box

This class defines the simulation box dimensions and boundaries, and keeps track of the simulation time step.

Parameters

sizetuple of float

Dimensions of the box as (width, height, depth).

Attributes

wfloat

Width of the box.

hfloat

Height of the box.

dfloat

Depth of the box.

sim_tsint

Current simulation time-step, initialized to 0.

leftfloat

Position of the left boundary, initialized to 0.

topfloat

Position of the top boundary, initialized to 0.

frontfloat

Position of the front boundary, initialized to 0.

rightfloat

Position of the right boundary, initialized to width.

bottomfloat

Position of the bottom boundary, initialized to height.

backfloat

Position of the back boundary, initialized to depth.

kanapy.core.entities.cub_oct_split(cub)

Splits cuboid object of the class Cuboid into eight smaller cuboid objects

Parameters:

cub (object of the class Cuboid) – Branch cuboid object containing ellipsoids

Returns:

Eight new sub-branch cuboid objects in a list

Return type:

List

Module collisions

kanapy.core.collisions.collide_detect(coef_i, coef_j, r_i, r_j, A_i, A_j)

Determines overlap between two static ellipsoids using the Algebraic Separation Condition developed by W. Wang et al., 2001. This function implements the method for two ellipsoids with given coefficients, positions, and rotation matrices

Parameters

coef_inumpy array

Coefficients of ellipsoid i

coef_jnumpy array

Coefficients of ellipsoid j

r_inumpy array

Position vector of ellipsoid i

r_jnumpy array

Position vector of ellipsoid j

A_inumpy array

Rotation matrix of ellipsoid i

A_jnumpy array

Rotation matrix of ellipsoid j

Returns

bool

True if ellipsoids i and j overlap, False otherwise

Notes

The method calculates the characteristic polynomial based on the ellipsoid coefficients and rigid body transformations. Roots of this polynomial are used with the Algebraic Separation Condition to determine whether the ellipsoids intersect. Real roots with negative values are analyzed to establish the overlap.

kanapy.core.collisions.collision_react(ell1, ell2)

Evaluates and modifies the magnitude and direction of the ellipsoid’s velocity after collision

Parameters

ell1Ellipsoid

Ellipsoid i

ell2Ellipsoid

Ellipsoid j

Notes

Consider two ellipsoids i, j at collision. Let them occupy certain positions in space defined by the position vectors r^i, r^j and have certain velocities represented by v^i, v^j respectively. The objective is to find the velocity vectors after collision. The elevation angle φ between the ellipsoids is determined by:

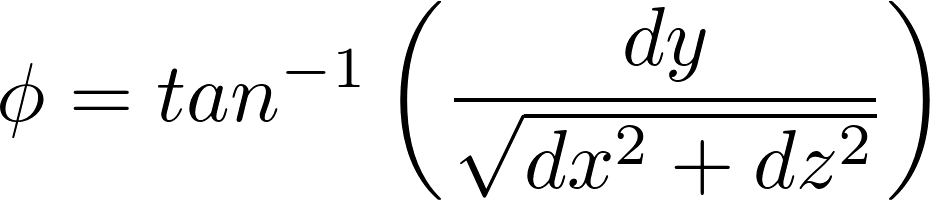
where dx, dy, dz are defined as the distance between the two ellipsoid centers along x, y, z directions given by:

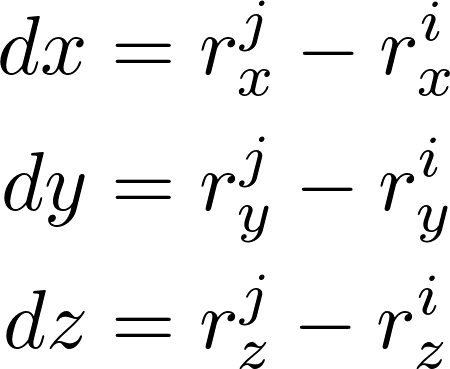
Depending on the magnitudes of dx, dz as projected on the x-z plane, the angle Θ is computed. The angles Θ and φ determine the in-plane and out-of-plane directions along which ellipsoid i would bounce back after collision. Thus, the updated velocity vector components along the x, y, z directions are determined by:

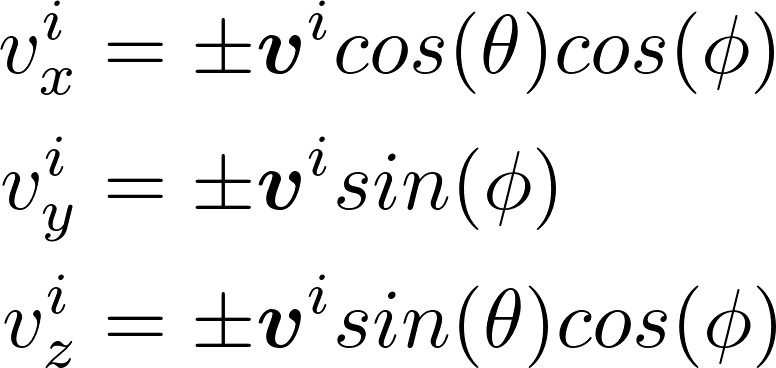
kanapy.core.collisions.collision_routine(E1, E2)

Detect and handle collision between two ellipsoid objects

Uses the algebraic separation condition by W. Wang et al. to detect overlap between two ellipsoids, and if a collision occurs, computes the contact response via the collision_react method.

Parameters

E1Ellipsoid

First ellipsoid object (particle i)

E2Ellipsoid

Second ellipsoid object (particle j)

Returns

bool

True if overlap (collision) is detected, False otherwise

Notes

• If both particles are spheres, the bounding sphere hierarchy alone suffices to detect collision.

• If either particle is an ellipsoid, their coefficients, positions, and rotation matrices are used in the overlap test.

Module voxelization

kanapy.core.voxelization.assign_voxels_to_ellipsoid(cooDict, Ellipsoids, voxel_dict, vf_target=None)

Assign voxels to each ellipsoid based on spatial position and shared nodes

Iteratively grows each ellipsoid and assigns voxels whose centers lie within the ellipsoid’s convex hull. Voxels are additionally checked to share at least 4 nodes with existing voxels of the ellipsoid to ensure connectivity.

Parameters

cooDictdict

Voxel dictionary containing voxel IDs as keys and center coordinates as values

Ellipsoidslist

List of ellipsoid objects from the packing routine. Each object must support .a, .b, .c attributes and .surfacePointsGen() and .get_pos() methods

voxel_dictdict

Element dictionary containing voxel IDs as keys and lists of nodal connectivity as values

vf_targetfloat, optional

Target volume fraction of particles to be assigned (default is 1.0)

kanapy.core.voxelization.points_in_convexHull(Points, hull)

Determine whether the given array of points lie inside the convex hull

Checks if each point in Points is inside or outside the convex hull defined by hull. Returns a boolean array with True for points inside the hull and False otherwise.

Parameters

Pointsndarray, shape (N_points, dim)

Array of points to be tested

hullscipy.spatial.ConvexHull

Convex hull object representing an ellipsoid or other shape

Returns

ndarray, shape (N_points,)

Boolean array indicating whether each point is inside the convex hull

See Also

https://stackoverflow.com/questions/21698630/how-can-i-find-if-a-point-lies-inside-or-outside-of-convexhull

kanapy.core.voxelization.reassign_shared_voxels(cooDict, Ellipsoids, voxel_dict)

Reassign shared voxels among ellipsoids to the most appropriate ellipsoid based on node overlap and proximity to ellipsoid centers

This function identifies voxels that are contained within multiple ellipsoids and resolves conflicts by: 1. Removing the shared voxel from all ellipsoids initially. 2. Assigning the voxel to the ellipsoid with the largest number of shared nodes. 3. If multiple ellipsoids have the same node overlap, assigning the voxel to the closest

ellipsoid based on center distance.

4. If still tied, assigning to the ellipsoid with the smallest volume.

Parameters

cooDictdict

Dictionary mapping voxel IDs to their coordinates in 3D space. Example: {voxel_id: [x, y, z], …}

Ellipsoidslist

List of ellipsoid objects from the packing routine. Each ellipsoid must have attributes: - inside_voxels (list of voxel IDs contained in the ellipsoid) - id (unique identifier) - get_pos() method returning the ellipsoid center coordinates as [x, y, z] - get_volume() method returning the ellipsoid volume

voxel_dictdict

Dictionary mapping voxel IDs to the node IDs that define the voxel. Example: {voxel_id: [node1, node2, …], …}

Notes

• The reassignment loop has a maximum of 5 cycles to avoid infinite loops in edge cases.

• A voxel is assigned to an ellipsoid only if it has at least 4 nodes in common with it.

• Distance calculations assume Cartesian coordinates.

• The function can handle ties in node overlap by considering proximity and volume.

• Modifies inside_voxels lists of ellipsoids in place.

kanapy.core.voxelization.voxelizationRoutine(Ellipsoids, mesh, nphases, prec_vf=None)

Perform voxelization of a microstructure defined by ellipsoids and mesh.

This function controls the voxelization process by calling several subroutines: - kanapy.input_output.read_dump() - create_voxels() - assign_voxels_to_ellipsoid() - reassign_shared_voxels()

Depending on whether ellipsoids have inner polygons, it either assigns voxels directly to ellipsoids or uses polygon-based voxel assignment.

The function also generates: - mesh.grains: array of voxelized structure with grain IDs - mesh.phases: array of voxelized structure with phase numbers - mesh.grain_dict: dictionary mapping grain IDs to voxel IDs - mesh.grain_phase_dict: dictionary mapping grain IDs to phase numbers - mesh.ngrains_phase: count of grains per phase - mesh.prec_vf_voxels: current volume fraction if prec_vf is provided

Parameters

Ellipsoidslist

List of ellipsoid objects representing grains. Each ellipsoid should have: - inside_voxels (list of voxel IDs) - duplicate (ID of original ellipsoid if duplicated, else None) - inner (optional polygon object) - phasenum (phase number) - get_pos() and create_poly() methods.

meshobject

Mesh object containing voxel information, including: - vox_center_dict (voxel centers) - voxel_dict (voxel-to-node mapping) - nvox (number of voxels) - dim (mesh dimensions)

nphasesint

Number of phases in the RVE.

prec_vffloat, optional

Target volume fraction for precipitates/porosity. Defaults to None (fully filled RVE).

Notes

• Voxels shared by multiple ellipsoids are resolved using reassign_shared_voxels.

• Voxels not assigned to any grain are either assigned to neighbors or set to phase 1.

• If prec_vf < 1.0, empty voxels are treated as dispersed phase (precipitates/porosity).

• The function modifies the mesh object in place.

Returns

mesh

The input mesh object with updated voxelized grain and phase information.

Module grains

Subroutines for analysis of grains in microstructure

@author: Alexander Hartmaier ICAMS, Ruhr University Bochum, Germany March 2024

kanapy.core.grains.calc_polygons(rve, mesh, tol=0.001)

Evaluates grain volumes and the shared surface area of grain boundaries between neighboring grains in a voxelized microstructure. Generates vertices at contact points where three or more grains meet and constructs polyhedral convex hulls for these vertices.

Parameters

rvekanapy object

Object containing information about the RVE geometry.

meshkanapy object

Object containing voxel mesh details and grain assignments for each voxel.

tolfloat, optional

Tolerance for numerical operations. Default is 1.e-3.

Returns

geometrydict

Dictionary containing the calculated geometrical information, including vertices, contact points, and convex hulls for grains.

Notes

For periodic structures, large grains spanning both halves of the simulation box and touching a boundary may be incorrectly split, which can affect geometry calculations.

Module rve_stats

Subroutines for analysis of statistical descriptors of RVEs:

• original particles (or their inner polyhedra)

• voxel structure

• polyhedral grain structure

@author: Alexander Hartmaier ICAMS, Ruhr University Bochum, Germany March 2024

kanapy.core.rve_stats.arr2mat(mc)

Convert a 6-element numpy array into a 3x3 symmetric matrix

Parameters

mcarray-like of length 6

Input array containing the elements of a symmetric matrix in Voigt notation: [M11, M22, M33, M23, M13, M12]

Returns

matndarray of shape (3, 3)

Symmetric 3x3 matrix corresponding to the input array

kanapy.core.rve_stats.bbox(pts, return_vector=False, two_dim=False)

Approximate the smallest rectangular cuboid around points of a grain

The function computes the principal axes and lengths of a cuboid that encloses the grain, allowing analysis of prolate (aspect ratio > 1) and oblate (aspect ratio < 1) particles. For 2D points, only two axes are returned.

Parameters

pts(N, dim) ndarray

Coordinates of points representing the grain

return_vectorbool, default=False

If True, return the unit vectors along each principal axis

two_dimbool, default=False

If True, treat points as 2D; otherwise, treat as 3D

Returns

If two_dim is True:

len_afloat

Semi-major axis length

len_bfloat

Semi-minor axis length

ax_a(dim,) ndarray, optional

Unit vector along major axis (only if return_vector=True)

ax_b(dim,) ndarray, optional

Unit vector along minor axis (only if return_vector=True)

If two_dim is False:

len_afloat

Semi-major axis length

len_bfloat

Semi-intermediate axis length

len_cfloat

Semi-minor axis length

ax_a(3,) ndarray, optional

Unit vector along major axis (only if return_vector=True)

ax_b(3,) ndarray, optional

Unit vector along intermediate axis (only if return_vector=True)

ax_c(3,) ndarray, optional

Unit vector along minor axis (only if return_vector=True)

kanapy.core.rve_stats.calc_stats_dict(a, b, c, eqd)

Calculate statistical descriptors of grain semi-axes and equivalent diameters

Computes log-normal parameters, identifies the rotation axis, and calculates aspect ratios for a set of grain semi-axes and equivalent diameters.

Parameters

andarray

Array of semi-axis a lengths

bndarray

Array of semi-axis b lengths

cndarray

Array of semi-axis c lengths

eqdndarray

Array of equivalent diameters

Returns

sddict

Dictionary containing sorted semi-axes, equivalent diameters, their log-normal parameters (sigma and scale), rotation axis index, aspect ratios, and related statistics

kanapy.core.rve_stats.con_fun(mc)

Constraint function: penalizes non-positive-definite matrices

For a symmetric matrix, all eigenvalues must be positive. This constraint returns a large negative value if the matrix has negative eigenvalues.

Parameters

mcarray-like of length 6

Input array representing a symmetric 3x3 matrix in Voigt notation

Returns

float

The smallest eigenvalue multiplied by 1000, serving as a penalty for negative eigenvalues

kanapy.core.rve_stats.find_rot_axis(len_a, len_b, len_c)

Determine the rotation axis of an ellipsoid based on its three semi-axes

The function identifies the axis of approximate rotational symmetry. If no clear symmetry is found, the longest axis is chosen as the rotation axis.

Parameters

len_afloat

Length of the first semi-axis

len_bfloat

Length of the second semi-axis

len_cfloat

Length of the third semi-axis

Returns

irotint

Index of the rotation axis (0 for a, 1 for b, 2 for c)

kanapy.core.rve_stats.get_diameter(pts)

Estimate the largest diameter of a set of points along Cartesian axes

Parameters

ptsndarray, shape (N, dim)

Point set in dim dimensions

Returns

diameterndarray, shape (dim,)

Vector connecting the two points with the largest separation along the axis of maximum extent

kanapy.core.rve_stats.get_grain_geom(points, method='raw', two_dim=False)

Fit an ellipse to the 2D convex hull of grain pixels

Depending on the chosen method, the ellipse can be obtained from direct fitting, PCA, or a rectangular bounding box. Currently, 3D grains are not supported.

Parameters

points(N, 2) ndarray

Coordinates of points on the grain hull

methodstr, default=’raw’

Method to obtain ellipse parameters: - ‘raw’: rectangular bounding box - ‘pca’: principal component analysis - ‘ell’, ‘ellipsis’, ‘e’: direct ellipse fitting

two_dimbool, default=False

If True, process as 2D data; 3D is not yet implemented

Returns

eafloat

Semi-major axis length (a >= b)

ebfloat

Semi-minor axis length

va(2,) ndarray

Unit vector along the major axis

vb(2,) ndarray

Unit vector along the minor axis

kanapy.core.rve_stats.get_ln_param(data)

Compute log-normal parameters (sigma and scale) from a dataset

This function calculates the parameters for a log-normal distribution by taking the logarithm of positive data points and computing the standard deviation and median-based scale.

Parameters

dataarray-like

Input data array. Values should be non-negative.

Returns

sigfloat

Standard deviation of the log-transformed data

scalefloat

Scale parameter of the log-normal distribution (exp of median)

kanapy.core.rve_stats.get_stats_part(part, iphase=None, ax_max=None, minval=1e-05, show_plot=True, verbose=False, save_files=False)

Extract statistics of particles and optionally their inner structures

Fits a 3D ellipsoid to each particle or its inner structure, calculates semi-axes, equivalent diameters, and statistical descriptors of the microstructure.

Parameters

partlist

List of particle objects, each with attributes a, b, c or inner.points

iphaseint, optional

Phase number to restrict analysis to, default is None (all phases)

ax_maxfloat, optional

Maximum allowed semi-axis, used to adjust minval for numerical stability

minvalfloat, optional

Minimum allowed eigenvalue for positive-definiteness, default 1.e-5

show_plotbool, optional

Whether to display plots of the statistics, default True

verbosebool, optional

If True, print detailed information during processing, default False

save_filesbool, optional

If True, save plots as files, default False

Returns

part_stats_dictdict

Dictionary containing semi-axes, equivalent diameters, log-normal parameters, rotation axis index, aspect ratios, and related statistics

kanapy.core.rve_stats.get_stats_poly(grains, iphase=None, ax_max=None, phase_dict=None, minval=1e-05, show_plot=True, verbose=False, save_files=False)

Extract statistics about the microstructure from polyhedral grains

Fits a 3D ellipsoid to each polyhedron to compute semi-axes, equivalent diameters, and other statistical descriptors.

Parameters

grainsdict

Dictionary of polyhedral grains with ‘Points’ for each grain

iphaseint, optional

Phase number to restrict analysis to, default is None (all phases)

phase_dictdict, optional

Dictionary mapping grain ID to phase number, required if iphase is provided

ax_maxfloat, optional

Maximum allowed semi-axis, used to adjust minval for numerical stability

minvalfloat, optional

Minimum allowed eigenvalue for positive-definiteness, default 1.e-5

show_plotbool, optional

Whether to display plots of the statistics, default True

verbosebool, optional

If True, print detailed information during processing, default False

save_filesbool, optional

If True, save plots as files, default False

Returns

poly_stats_dictdict

Dictionary containing semi-axes, equivalent diameters, log-normal parameters, rotation axis index, aspect ratios, and related statistics

kanapy.core.rve_stats.get_stats_vox(mesh, iphase=None, ax_max=None, minval=1e-05, show_plot=True, verbose=False, save_files=False)

Extract statistics of the microstructure from voxels

Analyses nodes at grain boundaries, constructs a rectangular bounding box, and calculates semi-axes, equivalent diameters, and statistical descriptors.

Parameters

meshobject

Mesh object containing grain and voxel information

iphaseint, optional

Phase number to restrict analysis to, default is None (all phases)

ax_maxfloat, optional

Maximum allowed semi-axis, used to adjust minval for numerical stability

minvalfloat, optional

Minimum allowed eigenvalue for positive-definiteness, default 1.e-5

show_plotbool, optional

Whether to display plots of the statistics, default True

verbosebool, optional

If True, print detailed information during processing, default False

save_filesbool, optional

If True, save plots as files, default False

Returns

vox_stats_dictdict

Dictionary containing semi-axes, equivalent diameters, log-normal parameters, rotation axis index, aspect ratios, and related statistics

kanapy.core.rve_stats.project_pts(pts, ctr, axis)

Project points to a plane defined by a center point and a normal vector

Parameters

ptsndarray, shape (N, dim)

Point set in dim dimensions

ctrndarray, shape (dim,)

Center point of the projection plane

axisndarray, shape (dim,)

Unit vector normal to the plane

Returns

pptndarray, shape (N, dim)

Points projected onto the plane

kanapy.core.rve_stats.pts_in_ellips(Mcomp, pts)

Check how well a set of points satisfy the equation of an ellipsoid (pts - ctr)^T M (pts - ctr) = 1

Parameters

Mcomparray-like, shape (6,)

Components of a symmetric matrix representing the ellipsoid.

ptsarray-like, shape (N, 3)

Coordinates of points to be tested.

Returns

scorefloat

Average deviation of points from the ellipsoid equation. Lower values indicate points are closer to lying on the ellipsoid surface.

Module texture

Tools for analysis of EBSD maps in form of .ang files

@author: Alexander Hartmaier, Abhishek Biswas, ICAMS, Ruhr-Universität Bochum

class kanapy.texture.DeLaValleePoussinKernel(kappa=None, halfwidth=None, bandwidth=None)

Bases: Kernel

De La Vallee Poussin kernel class for orientation distribution functions

Parameters

kappafloat, optional

Shape parameter of the kernel

halfwidthfloat, optional

Halfwidth in radians; overrides kappa if provided

bandwidthint, optional

Maximum degree of the series expansion

Attributes

Andarray

Series coefficients of the kernel

kappafloat

Shape parameter of the kernel

Cfloat

Normalization constant

DK(co2)

Evaluate the derivative of the De La Vallee Poussin kernel with respect to misorientation.

Parameters

co2float or ndarray

Cosine of half the misorientation angle. Values should be in [-1, 1].

Returns

float or ndarray

Derivative of the kernel function evaluated at the input co2.

DRK(t)

Evaluate the derivative of the reduced kernel function R_K at a given input.

Parameters

tfloat or ndarray

Input value, typically representing a normalized distance or cosine value.

Returns

float or ndarray

Value of the derivative of R_K at t.

K(co2)

Evaluate the De La Vallee Poussin kernel function.

Parameters

co2float or ndarray

Cosine of half the misorientation angle. Values will be clipped to [-1, 1].

Returns

float or ndarray

Kernel value(s) evaluated at the input co2.

RK(t)

Evaluate the reduced kernel function R_K at a given input.

Parameters

tfloat or ndarray

Input value, typically representing a normalized distance or cosine value.

Returns

float or ndarray

Value of the reduced kernel function R_K at t.

halfwidth()

Compute the halfwidth of the DeLaValleePoussin kernel.

The halfwidth is the misorientation angle ω where the kernel value drops to half its maximum.

Returns

float

Halfwidth angle in radians.

class kanapy.texture.EBSDmap(fname, gs_min=10.0, vf_min=0.03, max_angle=5.0, connectivity=8, show_plot=True, show_hist=None, felzenszwalb=False, show_grains=False, hist=None, plot=None)

Bases: object

Class to store attributes and methods to import EBSD maps and filter out their statistical data needed to generate synthetic RVEs

Parameters

fnamestr

Filename including path to EBSD file.

gs_minfloat, optional

Minimum grain size in pixels. Grains smaller than this are disregarded for statistical analysis. Default is 10.0.

vf_minfloat, optional

Minimum volume fraction. Phases with smaller values are disregarded. Default is 0.03.

max_anglefloat, optional

Maximum misorientation angle (degrees) used for grain merging. Default is 5.0.

connectivityint, optional

Connectivity for grain identification. Default is 8.

show_plotbool, optional

If True, plots microstructure maps. Default is True.

show_histbool, optional

If True, plots histograms of grain statistics. Default follows show_plot.

felzenszwalbbool, optional

If True, applies Felzenszwalb segmentation. Default is False.

show_grainsbool, optional

If True, plots grain labeling. Default is False.

histbool, optional

Deprecated. Use show_hist instead.

plotbool, optional

Deprecated. Use show_plot instead.

Attributes

emapobject

Loaded EBSD map object.

sh_x, sh_yint

Shape of EBSD map in pixels.

dx, dyfloat

Pixel size in microns.

npxint

Total number of pixels in the map.

ms_datalist of dict

Phase-specific microstructure information including: - name : str — phase name - vf : float — volume fraction - index : int — phase index - ori : Orientation — grain orientations - cs : crystal symmetry / Laue group - mo_map : ndarray — misorientation field - rgb_im : ndarray — IPF color image - ngrains : int — number of grains - gs_param, ar_param, om_param : ndarray — grain size, aspect ratio, main axis angle parameters - gs_data, ar_data, om_data : ndarray — raw distributions - gs_moments, ar_moments, om_moments : list — distribution moments - graph : object — microstructure graph

ci_mapndarray

Optional confidence index map if available.

ngrainsint

Total number of grains after merging/pruning.

calcORI(Ng, iphase=0, shared_area=None, nbins=12, res_low=5, res_high=25, res_step=2, lim=5, verbose=False, full_output=False)

Estimate optimum kernel half-width and produce reduced set of orientations for given number of grains

Parameters

Ngint

Numbr of grains for which orientation is requested.

iphaseint, optional

Phase for which data is requested. The default is 0.

shared_areaarray, optional

Grain boundary data. The default is None.

nbinsint, optional

number of bins for GB texture. The default is 12.

Returns

ori(Ng, 3)-array

Array with Ng Euler angles.

plot_ci_map()

Plot the confidence index (CI) map of the EBSD data if available

plot_felsenszwalb()

Apply Felzenszwalb segmentation to the misorientation map and plot the results

Notes

Segments the misorientation map using the Felzenszwalb algorithm and overlays the segment boundaries for visualization.

plot_grains(N=5)

Plot the N largest grains with one-hot maps, convex hulls, and principal axes

Parameters

Nint, optional

Number of largest grains to plot for each phase. Default is 5.

Notes

Each grain is visualized with its pixels, convex hull, and major/minor axes. Major axes are plotted in cyan, minor axes in green.

plot_grains_marked()

Plot grains with labels and major/minor axes for all phases

Notes

Each grain is annotated with its number. Major axes are plotted in black, minor axes in red. The plot uses a distinct colormap for different grains.

plot_graph()

Visualize the microstructure graph for all phases

Notes

Uses the visualize_graph function to display nodes and connections of each phase’s graph.

plot_ipf_map()

Plot the IPF (inverse pole figure) map for all phases

Notes

Pixels belonging to other phases are set to black. Each phase is visualized separately.

plot_mo_map()

Plot the misorientation map for all phases

Notes

Shows the misorientation angle of each pixel with respect to a reference orientation.

plot_pf(vector=None)

Plot pole figures for all phases using the specified sample direction

Parameters

vectorarray-like, optional

Sample reference vector for the pole figure. Default is [0, 0, 1].

Notes

Plots <111> poles in the sample reference frame for each phase.

plot_pf_proj(vector=None)

Plot projected pole figures for all phases using the specified sample direction

Parameters

vectorarray-like, optional

Sample reference vector for the projected pole figure. Default is [0, 0, 1].

Notes

Uses a projection method to visualize <111> poles in the sample reference frame.

plot_segmentation(show_mo=True, show_ipf=True)

Plot segmentation results for all phases

Parameters

show_mobool, optional

If True, overlay grain boundaries on the misorientation map. Default is True.

show_ipfbool, optional

If True, overlay grain boundaries on the IPF map. Default is True.

Notes

Uses similarity-based segmentation to highlight grain boundaries on the maps.

showIPF()

Plot the inverse pole figure (IPF) color key for all phases in the EBSD map

class kanapy.texture.Kernel(A=None)

Bases: ABC

Abstract base class for kernels used in orientation distribution estimation.

Attributes

Andarray

Flattened array of kernel parameters. Initialized to empty array if not provided.

K(co2)

Evaluate the kernel function at a given squared cosine value.

Parameters

co2float or ndarray

Cosine squared value(s), will be clipped to [-1, 1].

Returns

float or ndarray

Value(s) of the kernel function.

K_orientations(orientations_ref, orientations)

Evaluate the kernel function for the misorientation angles between two sets of orientations.

Parameters

orientations_refOrientation

Reference set of orientations.

orientationsOrientation

Target set of orientations to compare.

Returns

ndarray

Kernel values corresponding to misorientation angles.

RK(d)

Evaluate the kernel using the Clenshaw-L method for given cosine distances.

Parameters

darray_like

Cosine of angles (distance metric) in the range [-1, 1].

Returns

ndarray

Kernel values for the given distances.

RRK(dh, dr)

Evaluate the kernel on two sets of cosine distances using a reduced rotational kernel.

Parameters

dharray_like

Cosines of angles for the first set, clipped to [-1, 1].

drarray_like

Cosines of angles for the second set, clipped to [-1, 1].

Returns

ndarray

2D array of kernel values for each combination of dh and dr.

property bandwidth

Returns the bandwidth of the kernel.

The bandwidth is defined as the number of elements in A minus one.

Returns

int

Bandwidth of the kernel.

calc_fourier(L, max_angle=3.141592653589793, fft_accuracy=0.01)

Compute the Fourier coefficients of the kernel up to order L.

Parameters

Lint

Maximum order of the Fourier coefficients.

max_anglefloat, optional

Upper limit of integration in radians (default is pi).

fft_accuracyfloat, optional

Threshold below which coefficients are considered negligible and computation stops early (default is 1e-2).

Returns

ndarray

Array of Fourier coefficients of length <= L+1.

cutA(fft_accuracy=0.01)

Truncate the kernel array A based on the specified FFT accuracy.

Elements of A are scaled by 1/(l^2), and elements smaller than a threshold determined from fft_accuracy are removed.

Parameters

fft_accuracyfloat, optional

Desired FFT accuracy (default is 1e-2).

Notes

The first element is never truncated.

halfwidth()

Compute the halfwidth of the kernel.

The halfwidth is determined by finding the angle omega that minimizes the squared difference between K(1) and 2*K(cos(omega/2)).

Returns

float

Halfwidth angle in radians.

norm()

Compute the L2 norm of the squared kernel elements.

Returns

float

L2 norm of the squared elements of the kernel array A.

plot_K(n_points=200)

Plot the kernel function K as a function of misorientation angle.

Parameters

n_pointsint, optional

Number of points used for plotting the kernel function (default is 200).

class kanapy.texture.ODF(orientations, halfwidth=np.float64(0.17453292519943295), weights=None, kernel=None, exact=False)

Bases: object

Estimate an Orientation Distribution Function (ODF) from a set of orientations using kernel density estimation.

Parameters

orientationsorix.quaternion.Orientation

Input orientation set.

halfwidthfloat, optional

Halfwidth of the kernel in radians (default: 10 degrees).

weightsarray-like, optional

Weights for each orientation. If None, uniform weights are used.

kernelKernel instance, optional

Kernel function to use. If None, DeLaValleePoussinKernel is used.

exactbool, optional

If False and orientation count > 1000, approximation using grid is applied.

Attributes

orientationsorix.quaternion.Orientation

Orientation set stored in the ODF.

weightsndarray

Normalized weights of the orientations.

kernelKernel

Kernel used for density estimation.

halfwidthfloat

Halfwidth of the kernel in radians.

evaluate(ori)

Evaluate the ODF at given orientations.

Parameters

oriOrientation

Orientation(s) at which to evaluate the ODF.

Returns

valuesndarray

ODF values at the specified orientations.

kanapy.texture.build_graph_from_labeled_pixels(label_array, emap, phase, connectivity=8)

Build a graph representation of a microstructure from labeled pixels

Each node in the graph represents a grain (label) and stores pixel indices, average orientation, and orientation statistics. Edges connect neighboring grains based on pixel adjacency.

Parameters

label_arrayndarray of shape (H, W)

2D array of integer labels representing grains.

emapobject

Orientation map object containing: - rotations.data : orientation vectors for each pixel - phases.point_groups : symmetry information for each phase - dx, dy : pixel spacing in x and y directions

phaseint

Phase index to select the corresponding symmetry from emap.phases.point_groups.

connectivityint, optional

Connectivity criterion for neighbors (4 or 8). Default is 8.

Returns

networkx.Graph

Graph object with: - Nodes representing grains, storing ‘pixels’, ‘ori_av’, ‘ori_std’, ‘npix’ - Edges representing neighboring grains (shared boundaries) - Graph attributes: ‘label_map’, ‘symmetry’, ‘dx’, ‘dy’

Notes

• Uses summarize_labels to extract node properties from labeled pixels

• Loops over all pixels to add edges between neighboring grains

• The function preserves the shape and indices of label_array

kanapy.texture.calc_error(odf_ref, odf_test, res=10.0)

Compute the normalized difference between two orientation distribution functions (ODFs)

This function evaluates the ODFs on a sample grid in fundamental space and computes the L1 norm of the difference after normalization.

Parameters

odf_refobject

Reference ODF object. Must have .orientations.symmetry and .evaluate() method.

odf_testobject

Test ODF object to compare. Must have the same symmetry as odf_ref.

resfloat, optional

Resolution for sampling the fundamental space grid. Default is 10.

Returns

float

L1 error between the normalized ODFs.

Notes

• Raises a RuntimeError if the symmetries of the two ODFs do not match.

• Uses get_sample_fundamental to sample the fundamental zone and Orientation for evaluation.

• Does not modify the input ODFs.

kanapy.texture.calc_orientations(odf, nori, res=None)

Generate a set of orientations sampled from an orientation distribution function (ODF)

This function uses Monte Carlo sampling to generate nori orientations according to the probabilities defined by the input ODF. Sampling is performed in the fundamental zone of the crystal symmetry.

Parameters

odfobject

Orientation distribution function object. Must have .orientations.symmetry and .evaluate() method.

noriint

Number of orientations to generate.

resfloat, optional

Angular resolution in degrees for sampling the fundamental zone grid. If None, a resolution between 2° and 5° is selected based on ODF half-width.

Returns

Orientation

Orientation object containing nori orientations sampled from the ODF.

Notes

• Raises a RuntimeError if the Monte Carlo sampling does not converge after 200 iterations.

• Logs a warning if the SO3 grid resolution is too coarse for the requested number of orientations.

• Uses get_sample_fundamental to generate the sampling grid and Orientation to store results.

• Does not modify the input ODF.

kanapy.texture.createOriset(num, ang, omega, hist=None, shared_area=None, cs=None, degree=True, Nbase=10000, resolution=None, res_low=5, res_high=25, res_step=2, lim=5, verbose=False, full_output=False)

Create a set of Euler angles according to an ODF defined by input orientations and kernel half-width

Parameters

numint

Number of Euler angles to generate

ang(3,) or (M, 3) array or Orientation

Input set of Euler angles (in degrees or radians) defining the ODF

omegafloat

Kernel half-width (in degrees or radians)

histarray, optional

Histogram of MDF. Default is None

shared_areaarray, optional

Shared area between pairs of grains. Default is None

csSymmetry, optional

Crystal symmetry group. Default is ‘m3m’

degreebool, optional

If True, input angles and omega are in degrees. Default is True

Nbaseint, optional

Base number of orientations for artificial ODF. Default is 10000

resolutionfloat, optional

Resolution for orientation generation. If None, derived from omega

res_low, res_high, res_step, limint, optional

Parameters for texture reconstruction

verbosebool, optional

If True, prints progress messages. Default is False

full_outputbool, optional

If True, returns additional reconstruction outputs. Default is False

Returns

ori(num, 3) ndarray

Reduced set of Euler angles

Notes

Can generate artificial ODFs if input set is small. Grain-boundary-texture reconstruction with hist or shared_area requires the kanapy-mtex module.

kanapy.texture.createOrisetRandom(num, omega=None, hist=None, shared_area=None, cs=None, Nbase=None)

Create a set of Euler angles for a random texture

Parameters

numint

Number of Euler angles to generate

omegafloat, optional

Kernel half-width in degrees. Default is 7.5

histarray, optional

Histogram of MDF. Default is None

shared_areaarray, optional

Shared area between pairs of grains. Default is None

csSymmetry, optional

Crystal symmetry group. Default is ‘m3m’

Nbaseint, optional

Base number of orientations for random texture. Default is 5000

Returns

ori(num, 3) ndarray

Set of randomly distributed Euler angles

Notes

Unlike createOriset, this function directly generates num random orientations without reducing a larger artificial EBSD set. Grain-boundary-texture reconstruction using hist or shared_area requires the kanapy-mtex module.

kanapy.texture.export_graph(G, filename, format='graphml')

Export a microstructure graph to a file in the specified format

This function writes the NetworkX graph to disk in either GraphML or GEXF format.

Parameters

Gnetworkx.Graph

Graph object representing the microstructure.

filenamestr

Path to the output file.

formatstr, optional

File format for export. Supported options are ‘graphml’ and ‘gexf’. Default is ‘graphml’.

Notes

• Raises a ValueError if an unsupported format is provided

• Does not modify the graph

kanapy.texture.find_largest_neighbor(G, node)

Find the largest neighboring node of a given node in a graph

This function iterates over all neighbors of the specified node and returns the neighbor with the largest ‘npix’ (number of pixels).

Parameters

Gnetworkx.Graph

Graph object where nodes have an attribute ‘npix’ representing their size.

nodeint

Node ID for which the largest neighbor is to be found.

Returns

int

Node ID of the largest neighbor.

Notes

• Raises a ValueError if the node has no neighbors.

• Raises a ValueError if the graph contains circular edges (neighbor is the node itself).

• Does not modify the graph.

kanapy.texture.find_orientations_fast(ori1: Orientation, ori2: Orientation, tol: float = 0.001) → ndarray

Find closest matches in ori1 for each orientation in ori2 using KDTree

Parameters

ori1Orientation

Orientation database (e.g., EBSD orientations).

ori2Orientation

Orientations to match (e.g., grain mean orientations).

tolfloat

Angular tolerance in radians.

Returns

matchesnp.ndarray

Array of indices in ori1 matching each entry in ori2; -1 if no match found.

kanapy.texture.find_sim_neighbor(G, nn)

Find the neighboring node most similar in orientation to the given node

This function computes the misorientation angles between the given node and all its neighbors, and returns the neighbor with the smallest misorientation.

Parameters

Gnetworkx.Graph

Graph object where nodes have an ‘ori_av’ attribute representing average orientation. The graph also contains a ‘symmetry’ key in G.graph used for orientation calculations.

nnint

Node ID for which the most similar neighbor is to be found.

Returns

tuple

A tuple (neighbor_id, angle) where: - neighbor_id : int, ID of the neighbor with smallest misorientation - angle : float, misorientation angle with the given node

Notes

• Uses the Orientation class for misorientation calculations

• Assumes all neighbors have a valid ‘ori_av’ attribute

• Does not modify the graph

kanapy.texture.find_similar_regions(array, tolerance=0.087, connectivity=1)

Identify connected regions of similar values in a 2D array

This function labels all connected pixels in the input array whose values differ by at most tolerance. Connectivity can be 4- or 8-connected.

Parameters

arrayndarray of shape (H, W)

2D input array with values to segment.

tolerancefloat, optional

Maximum allowed difference between connected values. Default is 0.087.

connectivityint, optional

Connectivity criterion for neighbors: 1 for 4-connectivity, 2 for 8-connectivity. Default is 1.

Returns

labeled_arrayndarray of shape (H, W)

Array where each connected region of similar values has a unique label.

num_featuresint

Total number of connected regions found.

Notes

• Uses a depth-first search to find connected regions.

• Does not modify the input array.

• Assumes neighbors(i, j, connectivity) returns valid neighboring indices.

kanapy.texture.get_distinct_colormap(N, cmap='prism')

Generate N visually distinct colors as an RGB colormap.

Parameters: - N: int, number of colors - seed: optional int, random seed for reproducibility

Returns: - cmap: list of N RGB tuples in [0, 1]

kanapy.texture.get_ipf_colors(ori_list, color_key=0)

Get RGB colors for a list of orientations in radians

Parameters

ori_list(N, 3) ndarray

List of N Euler angles in radians

color_keyint, optional

Index of the IPF color key to use. Default is 0

Returns

colors(N, 3) ndarray

RGB values corresponding to each orientation

Notes

Assumes cubic crystal symmetry and cubic specimen symmetry

kanapy.texture.merge_nodes(G, node1, node2)

Merge the pixel and attribute data of node1 into node2 in a graph

This function performs the following steps: 1. Concatenates the pixel lists of node1 and node2 and updates node2’s ‘pixels’ attribute 2. Updates the average orientation ‘ori_av’ and pixel count ‘npix’ for node2 3. Updates the convex hull for node2 if it exists 4. Adds edges from node1’s neighbors to node2, avoiding duplicates 5. Removes node1 from the graph 6. Updates the graph’s ‘label_map’ to replace all occurrences of node1 with node2

Parameters

Gnetworkx.Graph

Graph object where nodes represent grains and have attributes: - ‘pixels’ : array of pixel indices - ‘ori_av’ : average orientation - ‘npix’ : number of pixels - optional ‘hull’ : ConvexHull object The graph also contains: - ‘label_map’ : 2D array of node labels - ‘dx’, ‘dy’ : pixel spacing in x and y directions

node1int

Node ID to be merged and removed

node2int

Node ID to merge into and retain

Notes

• Modifies the graph G in place

• Updates ‘pixels’, ‘ori_av’, ‘npix’, ‘hull’ for node2

• Updates ‘label_map’ to replace node1 with node2

• Adds new edges from node1 to node2 while avoiding duplicates

kanapy.texture.neighbors(r, c, connectivity=8)

Return the neighboring coordinates of a cell in a 2D grid.

Parameters

rint

Row index of the cell.

cint

Column index of the cell.

connectivityint, optional

Type of connectivity. Options are: - 1 or 4 : 4-connected neighbors (up, down, left, right) - 8 : 8-connected neighbors (includes diagonals) Default is 8.

Returns

neighborslist of tuple

List of (row, column) tuples representing neighboring cells.

Examples

>>> neighbors(2, 3, connectivity=4)
[(3, 3), (1, 3), (2, 4), (2, 2)]

>>> neighbors(2, 3)
[(3, 2), (3, 3), (3, 4), (2, 2), (2, 4), (1, 2), (1, 3), (1, 4)]

kanapy.texture.odf_est(ori, odf, nstep=50, step=0.5, halfwidth=None, verbose=False)

Estimate an ODF from a set of orientations using iterative half-width adjustment

This function generates a new orientation distribution function (ODF) from input orientations by iteratively adjusting the half-width to minimize the error relative to a reference ODF.

Parameters

oriOrientation

Input orientations used to estimate the ODF.

odfODF

Reference orientation distribution function for error comparison.

nstepint, optional

Maximum number of iterations for adjusting the half-width. Default is 50.

stepfloat, optional

Increment step in degrees for half-width adjustment. Default is 0.5.

halfwidthfloat, optional

Initial half-width in radians. If None, a value based on odf.halfwidth is used.

verbosebool, optional

If True, prints iteration details. Default is False.

Returns

ODF

Estimated orientation distribution function corresponding to input orientations.

Notes

• Uses calc_error to compare the estimated ODF with the reference ODF.

• Iteratively increases half-width until the error starts to increase.

• The returned ODF corresponds to the last half-width before error increased.

• Does not modify the input orientations or reference ODF.

kanapy.texture.plot_pole_figure(orientations, phase, vector=None, size=None, alpha=None)

Plot an inverse pole figure and pole density function for given orientations

This function visualizes the orientation distribution of a crystal phase by plotting the stereographic projection of specified poles and the corresponding pole density function (PDF).

Parameters

orientationsOrientation

Orientation object containing crystal orientations to plot.

phaseobject

Crystal phase object containing symmetry information and name.

vectorarray-like of shape (3,), optional

Miller indices of the pole vector to plot. Default is [0, 0, 1].

sizefloat, optional

Marker size for scatter plot. Automatically scaled if None.

alphafloat, optional

Marker transparency for scatter plot. Automatically scaled if None.

Notes

• Uses Matplotlib for plotting with stereographic projection.

• The first subplot shows the inverse pole figure (scatter of poles).

• The second subplot shows the pole density function.

• Marker size and transparency are scaled inversely with the number of orientations.

• Does not modify the input orientations or phase.

kanapy.texture.plot_pole_figure_proj(orientations, phase, vector=None, title=None, alpha=None, size=None)

Plot an inverse pole figure (IPF) projection and pole density function for EBSD data

This function visualizes crystal orientations along a specified sample direction using an IPF projection. The first subplot shows the scatter of rotated poles, and the second subplot shows the corresponding pole density function (PDF).

Parameters

orientationsOrientation

Orientation object containing crystal orientations to plot.

phaseobject

Crystal phase object with symmetry information and name.

vectorarray-like of shape (3,), optional

Sample direction to project (Miller indices). Default is [0, 0, 1].

titlestr, optional

Title for the plot. If None, automatically uses the principal axis of vector.

alphafloat, optional

Marker transparency for scatter plot. Automatically scaled if None.

sizefloat, optional

Marker size for scatter plot. Automatically scaled if None.

Notes

• Uses Matplotlib with stereographic projection (IPF) for plotting.

• Marker size and transparency are scaled inversely with the number of orientations.

• The first subplot shows the inverse pole figure (scatter of rotated poles).

• The second subplot shows the pole density function (PDF).

• Does not modify the input orientations or phase.

kanapy.texture.summarize_labels(label_array, rotations, wanted_labels=None)

Summarize labeled pixels with average orientation and statistics

This function computes, for each label in label_array (or a subset of wanted_labels): - Number of pixels - Pixel indices - Average orientation vector - Standard deviation of orientation

Parameters

label_arrayndarray of shape (H, W)

2D array of integer labels.

rotationsndarray of shape (H*W, D)

Orientation data corresponding to each pixel (e.g., emap.rotations.data).

wanted_labelssequence of int, optional

List of label IDs to summarize. If None, all labels in label_array are used.

Returns

list of tuples

Each tuple is (label, info_dict) where info_dict contains: - ‘npix’ : int, number of pixels - ‘pixels’ : array of 1D indices in label_array.ravel() - ‘ori_av’ : ndarray of shape (D,), average orientation vector - ‘ori_std’ : ndarray of shape (D,), standard deviation of orientation

Notes

• Uses np.add.reduceat and sorting for efficient computation

• The returned list preserves the order of wanted_labels if provided, otherwise follows sorted unique labels from label_array

• Does not modify input arrays

kanapy.texture.texture_reconstruction(ns, ebsd=None, ebsdfile=None, orientations=None, grainsfile=None, grains=None, kernel=None, kernel_halfwidth=5, res_low=5, res_high=25, res_step=2, lim=5, verbose=False)

Reconstruct a reduced ODF from EBSD or orientation data

This function systematically reconstructs an orientation distribution function (ODF) using a given number of orientations or grains in a representative volume element (RVE). The reconstructed ODF approximates the misorientation distribution of the input data. Follows the method described in Biswas et al. (https://doi.org/10.1107/S1600576719017138).

Parameters

nsint

Number of reduced orientations/grains in the RVE.

ebsdEBSDmap, optional

EBSD map containing orientations for a single phase.

ebsdfilestr, optional

Path to a *.mat file with EBSD data (not yet supported).

orientationsOrientation, optional

Predefined orientations to use instead of EBSD data.

grainsfilestr, optional

Path to estimated grains file (*.mat). Not used for kernel estimation.

grainsobject, optional

Grain data. Not used for kernel estimation.

kernelDeLaValleePoussinKernel, optional

Kernel for ODF estimation. Default: halfwidth=kernel_halfwidth.

kernel_halfwidthfloat, optional

Halfwidth in degrees for default DeLaValleePoussin kernel. Default is 5°.

res_lowfloat, optional

Minimum resolution (in degrees) of orientation grid for reconstruction. Default 5°.

res_highfloat, optional

Maximum resolution (in degrees) of orientation grid. Default 25°.

res_stepfloat, optional

Step size (in degrees) for grid resolution. Default 2°.

limint, optional

Maximum number of consecutive worsening errors before stopping. Default 5.

verbosebool, optional

If True, print progress and error information. Default False.

Returns

orired_fOrientation

Reduced set of orientations in the fundamental region.

odfred_fODF

Reconstructed ODF using the reduced orientations.

erofloat

L1 error between reference ODF and reconstructed ODF.

resfloat

Grid resolution (degrees) at which the minimum error was achieved.

Notes

• Uses Monte Carlo sampling and kernel smoothing to generate reduced orientations.

• Only supports single-phase EBSD data.

• Kernel estimation from grains or files is not yet supported; default kernel is used.

• The reconstructed ODF approximates the misorientation distribution of the input data.

kanapy.texture.visualize_graph(G, node_size=100, fs=12)

Visualize a microstructure graph using a spring layout

This function draws the nodes and edges of the graph with labels, using a spring layout for positioning. Node color, edge color, node size, and font size can be adjusted.

Parameters

Gnetworkx.Graph

Graph object representing the microstructure. Nodes should have meaningful labels.

node_sizeint, optional

Size of the nodes in the plot. Default is 100.

fsint, optional

Font size for node labels. Default is 12.

Notes

• Uses NetworkX’s spring_layout for node positioning

• Uses Matplotlib to render the plot

• Does not modify the graph

Module plotting

Subroutines for plotting of microstructures

Created on Mon Oct 4 07:52:55 2021

@author: Alexander Hartmaier, Golsa Tolooei Eshlaghi, Ronak Shoghi

kanapy.core.plotting.plot_ellipsoids_3D(particles, cmap='prism', dual_phase=None, silent=False, asp_arr=None, phases=False, cols=None)

Display ellipsoids after the packing procedure

Parameters

particleslist

List of ellipsoid objects representing particles in the microstructure.

cmapstr, optional

Color map for ellipsoids. Default is ‘prism’.

dual_phasebool, optional

Deprecated. Use phases instead. If True, ellipsoids are colored according to phase (red/green contrast).

silentbool, optional

If True, returns the figure object without displaying it. Default is False.

asp_arrlist of 3 floats, optional

Aspect ratio for the 3D axes (x, y, z). Default is [1, 1, 1].

phasesbool, optional

If True, ellipsoids are colored according to their phase number.

colslist of str, optional

List of colors used for each phase when phases=True.

Returns

figmatplotlib.figure.Figure, optional

The matplotlib figure object if silent=True.

Notes

• The dual_phase parameter is deprecated. Use phases to control coloring by phase.

• Each ellipsoid is represented by its surface mesh generated via surfacePointsGen method of the ellipsoid object.

kanapy.core.plotting.plot_init_stats(stats_dict, gs_data=None, ar_data=None, gs_param=None, ar_param=None, save_files=False, silent=False)

Plot initial microstructure descriptors (grain size and aspect ratio) based on user-defined statistics.

Parameters

stats_dictdict

Dictionary containing initial microstructure statistics. Expected keys: - “Equivalent diameter”: dict with ‘sig’, ‘scale’, optionally ‘loc’, ‘cutoff_min’, ‘cutoff_max’ - “Aspect ratio”: dict with ‘sig’, ‘scale’, optionally ‘loc’, ‘cutoff_min’, ‘cutoff_max’ (for elongated grains) - “Grain type”: str, one of “Equiaxed”, “Elongated”, or “Free” - “Semi axes”: dict with ‘scale’, ‘sig’, ‘cutoff_min’, ‘cutoff_max’ (for free grains) - “Phase”: dict with ‘Number’ and ‘Name’, optional

gs_dataarray-like, optional

Experimental equivalent diameter data. Default is None.

ar_dataarray-like, optional

Experimental aspect ratio data. Default is None.

gs_paramtuple, optional

Parameters (s, loc, scale, min, max) for lognormal distribution of experimental equivalent diameters. Default is None.

ar_paramtuple, optional

Parameters (s, loc, scale, min, max) for lognormal distribution of experimental aspect ratios. Default is None.

save_filesbool, optional

If True, save the figure to file “Input_distribution.png”. Default is False.

silentbool, optional

If True, return the figure object instead of displaying it. Default is False.

Returns

figmatplotlib.figure.Figure, optional

The figure object if silent=True.

Notes

• The function automatically selects plotting style depending on “Grain type”:

  • “Equiaxed”: only equivalent diameter distribution

  • “Elongated”: both equivalent diameter and aspect ratio distributions

  • “Free”: compute aspect ratio from semi-axes and rotation axis

• Vertical dashed lines mark the minimum and maximum cut-offs from stats_dict.

• Overlays experimental data (histogram) and lognormal fits if gs_data or ar_data are provided.

• Uses lognormal PDFs for both grain size and aspect ratio.

kanapy.core.plotting.plot_output_stats(data_list, labels, iphase=None, gs_data=None, gs_param=None, ar_data=None, ar_param=None, save_files=False, silent=False, enhanced_plot=False)

Evaluate and plot particle- and RVE grain statistics, including equivalent diameters and aspect ratios

Parameters

data_listlist of dict

List of dictionaries containing particle/grain statistics. Each dictionary should include keys like ‘eqd’, ‘eqd_scale’, ‘eqd_sig’, ‘ar’, ‘ar_scale’, ‘ar_sig’.

labelslist of str

Labels indicating the type of data in data_list, e.g., [‘Grains’, ‘Partcls’].

iphaseint, optional

Phase index to label the plots. Default is None.

gs_dataarray-like, optional

Experimental equivalent diameter data for comparison. Default is None.

gs_paramtuple, optional

Parameters for lognormal distribution of experimental data (s, loc, scale). Default is None.

ar_dataarray-like, optional

Experimental aspect ratio data for comparison. Default is None.

ar_paramtuple, optional

Parameters for lognormal distribution of experimental aspect ratio data (s, loc, scale). Default is None.

save_filesbool, optional

If True, saves the generated figures as PNG files. Default is False.

silentbool, optional

If True, returns the figure objects instead of showing them. Default is False.

enhanced_plotbool, optional

If True, produces higher-resolution comparison plots using lognormal PDFs. Default is False.

Returns

figmatplotlib.figure.Figure, optional

Figure object if silent=True.

Notes

• The function can compare statistical distributions between grains, particles, and experimental data.

• Both histograms and lognormal probability density functions are used to display distributions.

• If enhanced_plot=True, PDFs for equivalent diameter and aspect ratio are plotted using a dense x-axis.

• labels must contain at least ‘Grains’ or ‘Voxels’. Otherwise, a ValueError is raised.

kanapy.core.plotting.plot_particles_3D(particles, cmap='prism', dual_phase=False, plot_hull=True, silent=False, asp_arr=None)

Display inner polyhedra and optional hulls of ellipsoids after packing procedure

Parameters

particleslist

List of ellipsoid objects containing inner polygons and convex hulls.

cmapstr, optional

Colormap for ellipsoids. Default is ‘prism’.

dual_phasebool, optional

If True, colors ellipsoids according to phase (red/green contrast).

plot_hullbool, optional

If True, plots the outer hull of the ellipsoid. Default is True.

silentbool, optional

If True, returns the figure object instead of displaying the plot.

asp_arrlist of 3 floats, optional

Aspect ratio for the 3D axes (x, y, z). Default is [1, 1, 1].

Returns

figmatplotlib.figure.Figure, optional

Matplotlib figure object if silent=True.

Notes

• Each ellipsoid must have an inner polygon (pa.inner) to be plotted.

• The convex hull of the ellipsoid is displayed using plot_trisurf.

• If plot_hull is True, the outer surface of the ellipsoid is also plotted using plot_surface.

kanapy.core.plotting.plot_polygons_3D(geometry, cmap='prism', alpha=0.4, ec=None, dual_phase=None, silent=False, asp_arr=None, phases=False, cols=None)

Plot triangularized convex hulls of grains based on vertices and simplices

Parameters

geometrydict

Dictionary containing grain geometry with keys: - ‘Grains’: dict with simplices (triangles) for each grain - ‘Points’: ndarray of vertex coordinates (N, 3)

cmapstr, optional

Colormap for coloring the triangles. Default is ‘prism’.

alphafloat, optional

Transparency of the polygons. Default is 0.4.

eccolor or list, optional

Edge color for triangles. Default is [0.5, 0.5, 0.5, 0.1].

dual_phasebool, optional

Deprecated. Use phases instead. If True, grains are colored by phase in red/green contrast.

silentbool, optional

If True, returns the figure object instead of showing it. Default is False.

asp_arrlist of 3 floats, optional

Aspect ratio for the 3D axes (x, y, z). Default is [1, 1, 1].

phasesbool, optional

If True, colors grains according to their phase number.

colslist of str, optional

Colors to use for each phase when phases=True.

Returns

figmatplotlib.figure.Figure, optional

Matplotlib figure object if silent=True.

Notes

• The dual_phase parameter is deprecated. Use phases to control coloring by phase.

• Each grain is plotted using its convex hull triangles defined in geometry[‘Grains’][igr][‘Simplices’].

kanapy.core.plotting.plot_stats_dict(sdict, title=None, save_files=False)

Plot statistical data on semi-axes of effective ellipsoids in RVE as histogram

Parameters

sdictdict

Dictionary containing semi-axis data and log-normal parameters. Keys should include ‘a’, ‘b’, ‘c’, and their corresponding ‘_sig’ and ‘_scale’.

titlestr, optional

Title for the plot

save_filesbool, optional

Whether to save the plot as PNG in the current working directory

kanapy.core.plotting.plot_voxels_3D(data, Ngr=None, sliced=False, dual_phase=None, mask=None, cmap='prism', alpha=1.0, silent=False, clist=None, asp_arr=None, phases=False, cols=None)

Plot voxels in microstructure, each grain with a different color. Sliced indicates whether one eighth of the box should be removed to see internal structure. With alpha, the transparency of the grains can be adjusted.

Parameters

dataint array

Grain number or phase number associated to each voxel

Ngrint, optional

Number of grains. The default is 1.

slicedBoolean, optional

Indicate if one eighth of box is invisible. The default is False.

dual_phaseBoolean, optional

Indicate if microstructure is dual phase. The default is False.

maskbool array, optional

Mask for voxels to be displayed. The default is None, in which case all voxels will be plotted (except sliced).

cmapcolor map, optional

Color map for voxels. The default is ‘prism’.

alphafloat, optional

Adjust transparency of voxels in alpha channel of color map. The default is 1.0.

showbool

Indicate whether to show the plot or to return the axis for further use

clist(Ngr, 3)-ndarray

List of RGB colors for each grain

Returns

axmatplotlib.axes

Axes handle for 3D subplot

Module smoothing

class kanapy.core.smoothingGB.Node(iden, px, py, pz)

Bases: object

Class representing a single node in 3D space with position, velocity, acceleration, and anchors

Parameters

idenint

Identifier to assign to the node

pxfloat

Initial x-coordinate of the node

pyfloat

Initial y-coordinate of the node

pzfloat

Initial z-coordinate of the node

Attributes

idint

Unique identifier of the node

px, py, pzfloat

Current x, y, z coordinates of the node

oripx, oripy, oripzfloat

Original x, y, z coordinates of the node

vx, vy, vzfloat

Velocity components along x, y, z

ax, ay, azfloat

Acceleration components along x, y, z

anchorslist

List of anchors connected to this node

Notes

This class represents a single node in 3D space, storing both its kinematic state (position, velocity, acceleration) and connections to anchors.

compute_acc(fx, fy, fz, mass)

Compute the acceleration of the node given applied forces and mass

Parameters

fxfloat

Force component along x

fyfloat

Force component along y

fzfloat

Force component along z

massfloat

Mass of the node

get_Oripos()

Return the original position of the node as a NumPy array

Returns

oriposndarray

Array containing the original x, y, z coordinates of the node

get_pos()

Return the current position of the node as a NumPy array

Returns

posndarray

Array containing the x, y, z coordinates of the node

get_vel()

Return the current velocity of the node as a NumPy array

Returns

velndarray

Array containing the velocity components vx, vy, vz

update_pos(dt)

Update the position of the node based on its velocity and time step

Parameters

dtfloat

Time step for the update

update_vel(dt)

Update the velocity of the node based on its acceleration and time step

Parameters

dtfloat

Time step for the update

kanapy.core.smoothingGB.initalizeSystem(nodes_v, grain_facesDict)

Initialize a spring-mass system from nodes and grain faces

Creates Node objects for all nodes, generates anchors at the center of each face, and links nodes to their associated anchors for the spring-mass system.

Parameters

nodes_vndarray

Array of nodal coordinates with shape (Nnodes, 3)

grain_facesDictdict

Dictionary mapping grain ID to a dictionary of outer faces, as returned by readGrainFaces

Returns

allNodeslist of Node

List of Node objects with anchors assigned

anchDictdict

Dictionary mapping face ID to anchor position (x, y, z)

kanapy.core.smoothingGB.readGrainFaces(nodes_v, elmtDict, elmtSetDict)

Extract outer faces of polyhedral grains from voxel connectivity

Constructs a dictionary of outer faces for each grain by analyzing voxel elements, excluding faces that lie on the boundary of the RVE.

Parameters

nodes_vndarray

Array of nodal coordinates with shape (Nnodes, 3)

elmtDictdict

Dictionary mapping element ID to its 8 node indices

elmtSetDictdict

Dictionary mapping grain ID to a list of element IDs belonging to that grain

Returns

grain_facesDictdict

Dictionary mapping grain ID to a dictionary of outer faces. Each face is stored as {face_id: [node1, node2, node3, node4]}.

kanapy.core.smoothingGB.relaxSystem(allNodes, anchDict, dt, N, k, c, RVE_xmin, RVE_xmax, RVE_ymin, RVE_ymax, RVE_zmin, RVE_zmax)

Relax the spring-mass system to reach equilibrium

Integrates the motion of nodes over N time steps with time step dt, considering spring forces to anchors and damping. Boundary nodes at RVE surfaces are fixed in the corresponding directions.

Parameters

allNodeslist of Node

List of Node objects with positions, velocities, and anchors

anchDictdict

Dictionary mapping face ID to anchor position (x, y, z)

dtfloat

Time step for integration

Nint

Number of integration steps

kfloat

Spring stiffness

cfloat

Damping coefficient

RVE_xmin, RVE_xmaxfloat

Minimum and maximum x-coordinates of RVE boundary

RVE_ymin, RVE_ymaxfloat

Minimum and maximum y-coordinates of RVE boundary

RVE_zmin, RVE_zmaxfloat

Minimum and maximum z-coordinates of RVE boundary

Returns

allNodeslist of Node

Updated list of Node objects after relaxation

kanapy.core.smoothingGB.smoothingRoutine(nodes_v, elmtDict, elmtSetDict)

Smooth a voxel-based microstructure by relaxing a spring-mass-anchor system

Constructs outer faces of grains, initializes nodes with anchors at face centers, and iteratively relaxes the system to reduce irregularities in node positions.

Parameters

nodes_vndarray, shape (N_nodes, 3)

Coordinates of all nodes in the voxel mesh

elmtDictdict

Dictionary mapping element ID to its node indices

elmtSetDictdict

Dictionary mapping grain ID to the set of element IDs it contains

Returns

nodes_sndarray, shape (N_nodes, 3)

Smoothed coordinates of all nodes

grain_facesDictdict

Dictionary mapping grain ID to its outer faces and corresponding node connectivity